Probability is a mathematical tool used to study randomness and provide predictions about the likelihood of something happening. There are several basic rules of probability that can be used to help determine the probability of multiple events happening together, separately, or sequentially. This article covers the fundamentals of probability, which are important both when conducting or interpreting the results of clinical trials, and when making clinical decisions for patients Patients Individuals participating in the health care system for the purpose of receiving therapeutic, diagnostic, or preventive procedures. Clinician–Patient Relationship based on the probability of different outcomes.
Last updated: Sep 12, 2022
Probability is a mathematical tool used to study randomness and provide predictions about the likelihood of something happening.
Example of probability:
If you toss a fair coin, the theoretical probability of heads on any given toss is 50%.
Example of short-term vs long-term outcomes:
If you toss a fair coin, there is a 50% chance of getting heads on any given toss. If you toss 10 heads in a row, this does not increase the chance of getting heads on the next toss (a short-term outcome). The LLN does mean Mean Mean is the sum of all measurements in a data set divided by the number of measurements in that data set. Measures of Central Tendency and Dispersion that over a large number of coin tosses, the frequency of getting heads will be close to 50%.
The probability of an event (A) happening is between 0 (absolute certainty of it not occurring) and 1 (absolute certainty of it occurring):
$$ 0\leq P(A)\leq 1 $$Summation of all the probabilities of all possible outcomes in a sample space add up to 1:
$$ P(S) = 1 $$Random phenomena are situations where the possible outcomes are known, but the one that will happen is unknown.
Some events only have 2 possible outcomes: event A occurs, or event A does not occur. The complement of event A is that event A does not occur, and is represented as AC. The probability of AC occurring equals 1 minus the probability of the event itself (A).
$$ P(A^{C}) = 1 – P(A) $$
A Venn diagram illustrating the complement rule:
The entire gray box represents the sample space, which equals 1. Event A represents 1 portion of the box, and event A not occurring represents the remaining portion of the sample space. From the “Introduction to Probability” lecture
Example: You have a 1-in-4 chance of drawing a club from a standard deck of cards. What is the probability that you will not draw a club?
Answer: In this example, drawing a club is event A and not drawing a club is AC. If the chance of drawing a club is 0.25, then AC = 1 ‒ 0.25, which is 0.75.
If 2 or more events cannot occur simultaneously, they are called mutually exclusive or disjoint events. While it is not possible for the 2 disjoint events to occur simultaneously, it is possible for neither of them to occur.
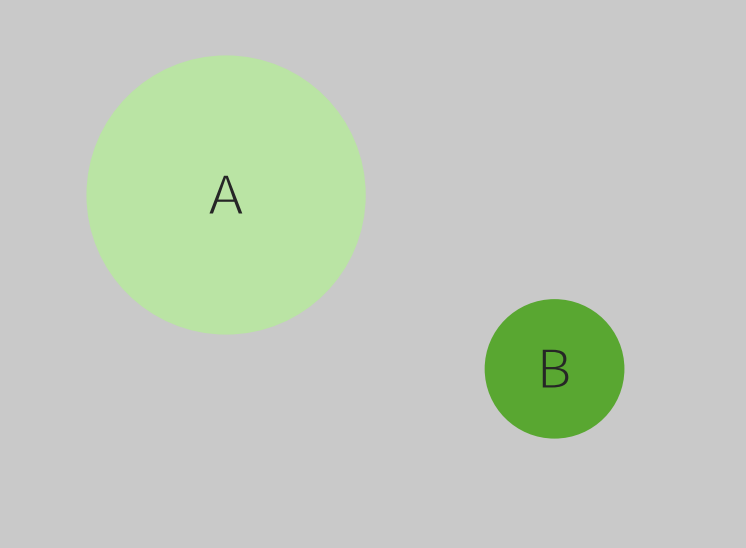
A Venn diagram illustrating the rule of disjoint events:
The area of the box represents the entire sample space, which equals 1. Circle A represents the probability of event A occurring, and circle B represents the probability of event B occurring.
The circles do not overlap, indicating they are mutually exclusive and cannot occur simultaneously. It is possible, however, for neither event to occur. Notice how they do not overlap.
When 2 events (A and B) are mutually exclusive (or disjoint), the probability that A or B will occur is the sum of the probability of each event.
$$ P(A\cup B) = P(A) + P(B) $$This rule can be applied to any number of disjoint events. For instance, to find the probability of either A, B, or C occurring, you can simply add P(A) + P(B) + P(C), assuming all 3 are completely mutually exclusive events.
Example 1:
Example 2:
Events are independent when the probability of one does not affect that of the other (Note: Disjoint events cannot be independent events (Example 2)). The probability of 2 independent events both occurring equals the product Product A molecule created by the enzymatic reaction. Basics of Enzymes of the probabilities of events A and B.
$$ P(A\cap B) = P(A)P(B) $$Example 1:
Example 2: Disjoint events cannot be independent of each other
The probability of an event (A), or another event (B), or both happening is given by the equation:
$$ P(A\cup B) = P(A) + P(B) – P(A\cap B) $$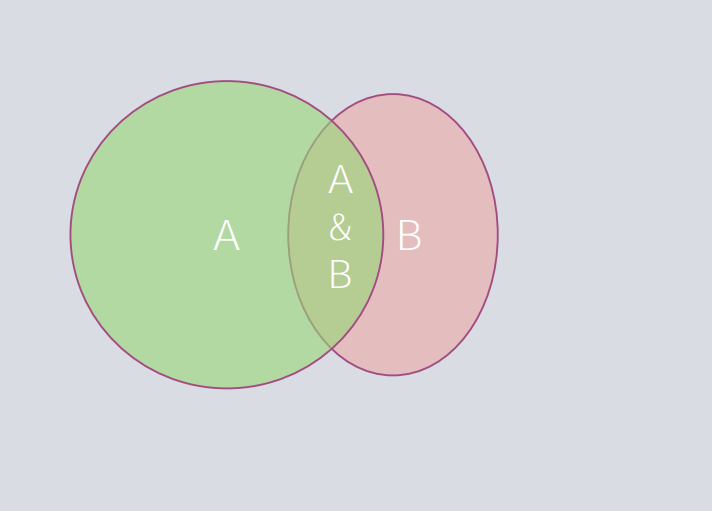
A Venn diagram illustrating the general addition rule of probability:
The area of the entire gray box represents the entire sample space, which equals 1. There is a circle that encapsulates the probability of event A occurring (green), and another for event B (red). The area where they overlap represents the probability of both events occurring simultaneously.
Therefore, if you were to simply add the area of the green circle to that of the red circle, the overlapped area would be counted twice. Visually, the total probability of either A, B, or both occurring can be represented as P(A) + [P(B) ‒ P(A&B)].
Example: You have a stack of money with 4 bill denominations: $1, $5, $10, and $20. Event A represents drawing an odd-numbered bill; event B represents drawing a bill between $4 and $12. What is the probability of A or B happening?
Answer: Note that $5 is in both events; therefore, they are not disjoint or mutually exclusive. Thus, we cannot simply add P(A) + P(B), because we will have counted the probability of a $5 bill being drawn (P($5)) twice. We, therefore, must subtract P($5) so that it is only counted once in the end. If the chances of drawing each bill are the same, then the probability of drawing each individual bill is 1 in 4, or 25%.
So, to answer our question, 1st we can calculate P(A), which equals P($1) + P($5) = 0.25 + 0.25 = 0.5. Similarly, P(B) = P($5) + P($10) = 0.25 + 0.25 = 0.5. We know that P($5) by itself is 0.25. So, overall, 0.5 + 0.5 ‒ 0.25 = 0.75, which represents 3 out of the 4 bills (the $1, $5, and $10 bills, which are all included in either event A or B).