Start your online calculus course
with Batool Akmal from Cardiff University, UK
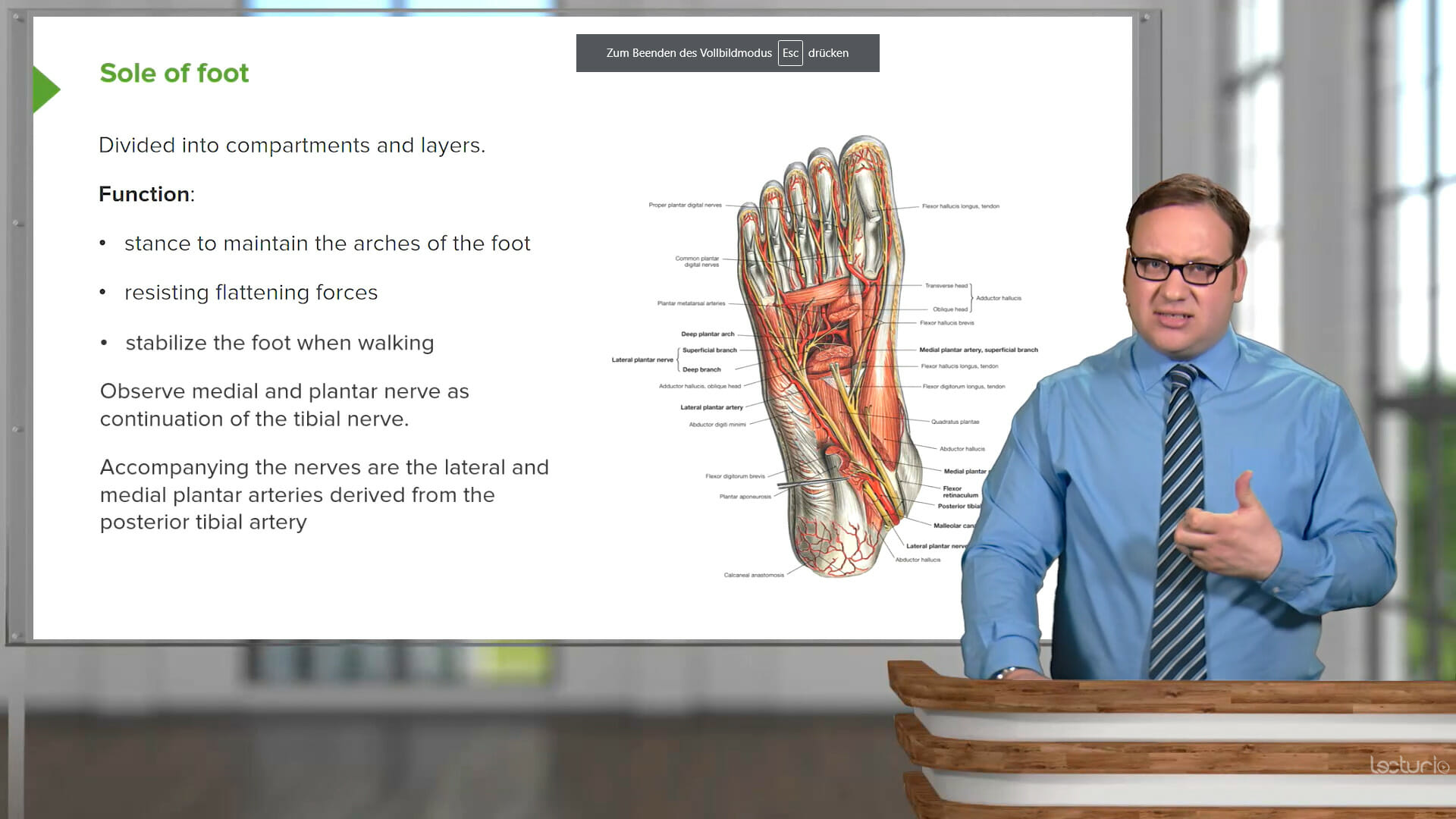
Calculus is the backbone of many medical technologies and quantitative analyses. Mastering mathematical thinking is not only necessary to excel on the MCAT; but to make trustworthy observations when caring for patients. However, grasping mathematical concepts and applying them to medical problems is a significant hurdle for many premed students on their path to medical school.
This course covers key calculus topics including gradients, differentiation in trigonometry, implicit and parametric differentiation, exponential and logarithmic functions, and advanced integration techniques. Batool Akmal, an esteemed educator from Cardiff University, will teach you to navigate complex mathematical methods and guide you through their practical application in medicine.
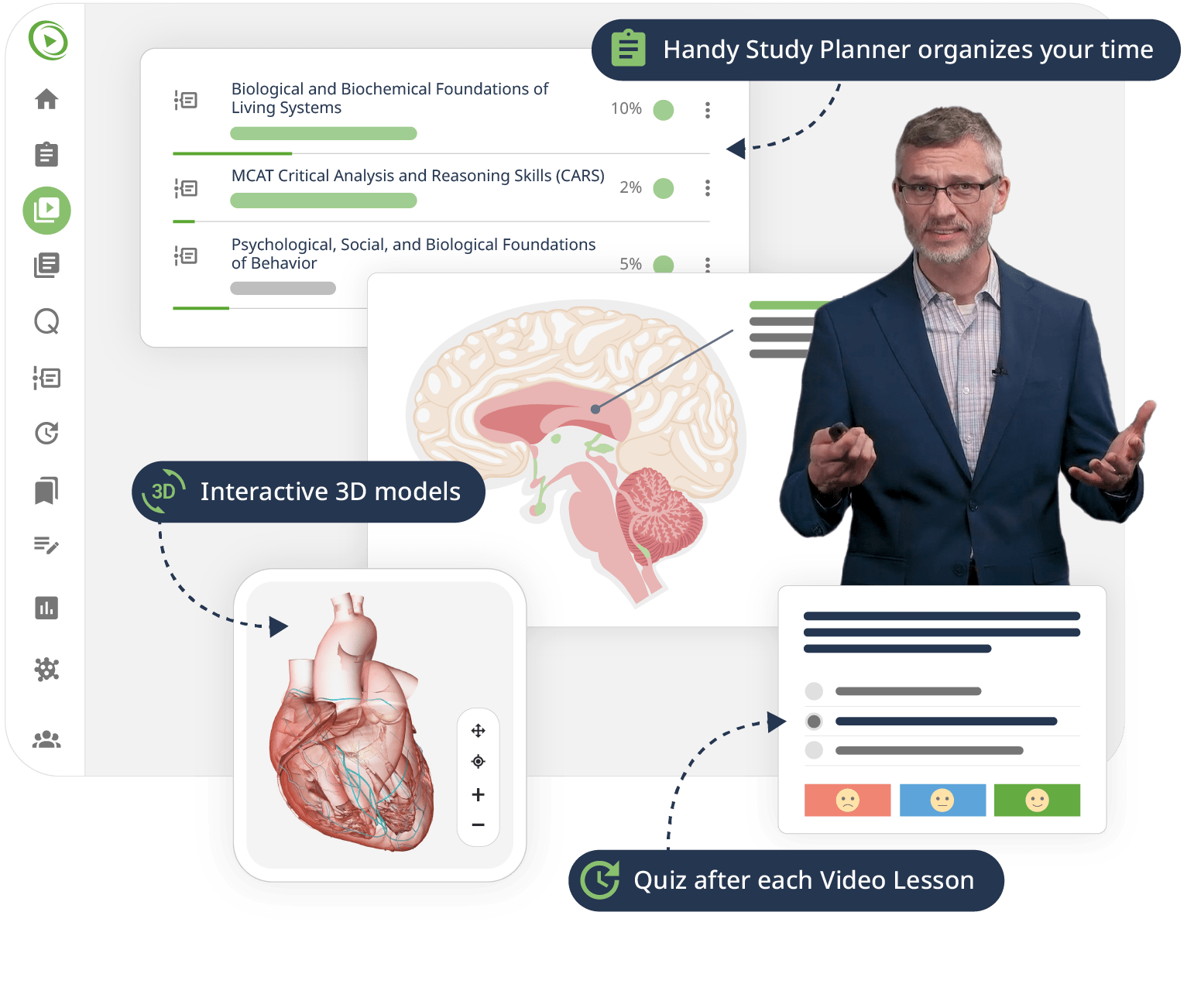
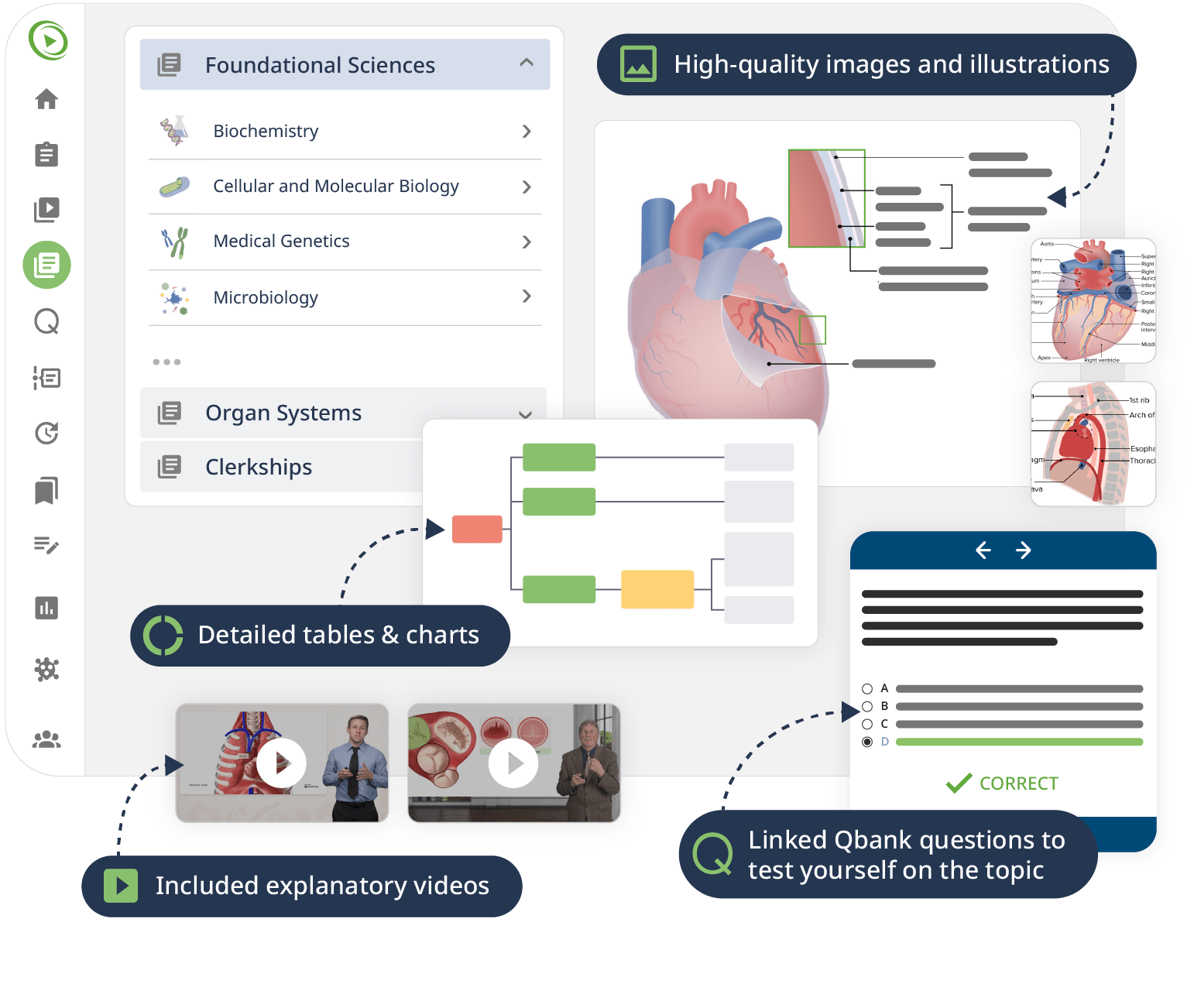
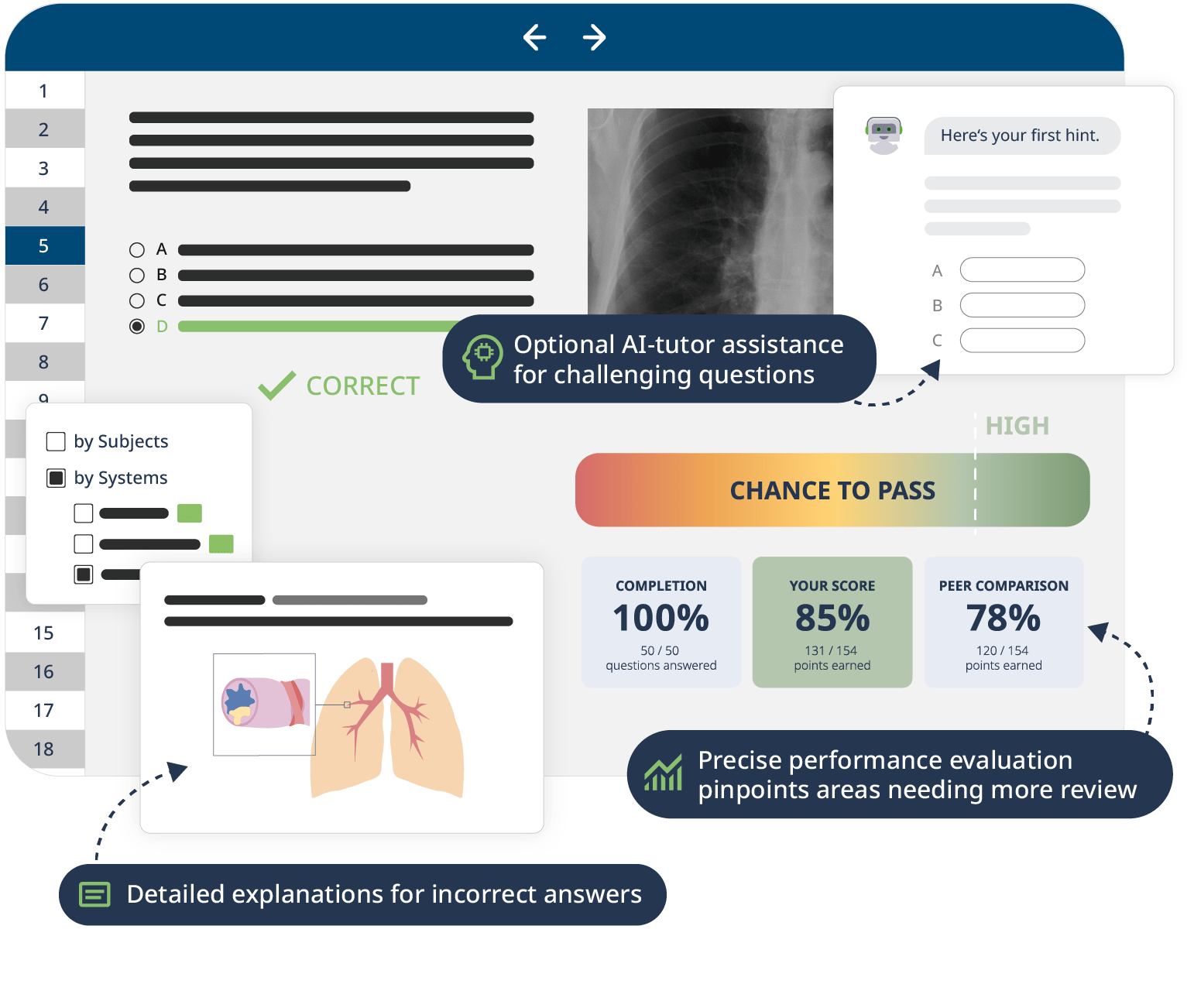
Interactive quiz questions, downloadable study materials, and a MCAT-style Qbank support your learning by boosting retention and understanding. By the end of this course, you will confidently apply calculus methods to medical scenarios, preparing you to ace the MCAT as well as setting you up for a successful career in medicine.