Um dos principais objetivos da investigação e dos estudos médicos é perceber quais as associações ou os resultados não resultam do acaso. De acordo com o desenho do estudo e os dados que este fornece, pode aceitar-se ou rejeitar-se uma hipótese, permitindo a determinação de uma correlação. Os testes estatísticos são ferramentas usadas por investigadores para obter informação e significados de conjuntos de dados variáveis. Estes testes vêm em várias formas, incluindo, por exemplo, os testes qui-quadrado e exatos de Fisher, e são escolhidos dependendo das necessidades dos investigadores e das características das variáveis analisadas. Os resultados do estudo podem ser considerados estatisticamente significativos com base em p-values calculados e níveis de significância predeterminados (conhecidos como nível α). Os intervalos de confiança são outra forma de expressar a significância de um resultado estatístico sem usar um p-value.
Última atualização: Aug 1, 2022
O teste de hipóteses é usado para avaliar a plausibilidade de uma hipótese através da análise dos dados do estudo.
Por exemplo, uma empresa cria um novo fármaco X destinado ao tratamento da hipertensão. A empresa quer saber se o fármaco X de facto funciona para baixar a PA, pelo que precisa de fazer testes de hipóteses.
Passos para testar uma hipótese:
Uma hipótese é uma resposta preliminar a uma questão de investigação (ou seja, uma “suposição” sobre quais serão os resultados). Existem 2 tipos de hipóteses: a hipótese nula e a hipótese alternativa.
Exemplo 1: rejeitar a hipótese nula
No exemplo acima, se os resultados do ensaio demonstrarem que o fármaco X de facto reduz significativamente a PA (ou seja, existe evidência estatística suficiente para o suportar), então a hipótese nula (postulando que não há diferença entre os grupos) é rejeitada com uma determinada probabilidade. Note-se que estes resultados não podem confirmar a hipótese alternativa, mas apenas a suportam com uma dada probabilidade, determinada pela distribuição da amostra na população testada
Exemplo 2: não rejeitar a hipótese nula
No exemplo acima, se os resultados do ensaio demonstrarem que o fármaco X não baixou significativamente a PA, então o estudo não rejeitou a hipótese nula. Mais uma vez, note-se que os resultados não podem confirmar a hipótese nula, mas apenas suportá-la com uma dada probabilidade, determinada pela distribuição da amostra na população testada.
A significância estatística é a ideia de que é altamente improvável que todos os resultados dos testes sejam produzidos simplesmente por acaso. Para determinar a significância estatística, é preciso definir um valor α e calcular um valor p (p-value).
Pode ser criado um gráfico no qual os possíveis resultados do estudo são colocados no eixo x e a probabilidade de observar cada resultado é colocada no eixo y. A área sob a curva representa o valor de p (p-value).
Mnemónica:
“If the p is low, the null (hypothesis) must go.” (Se o p for baixo, o nulo (hipótese) deve desaparecer.)
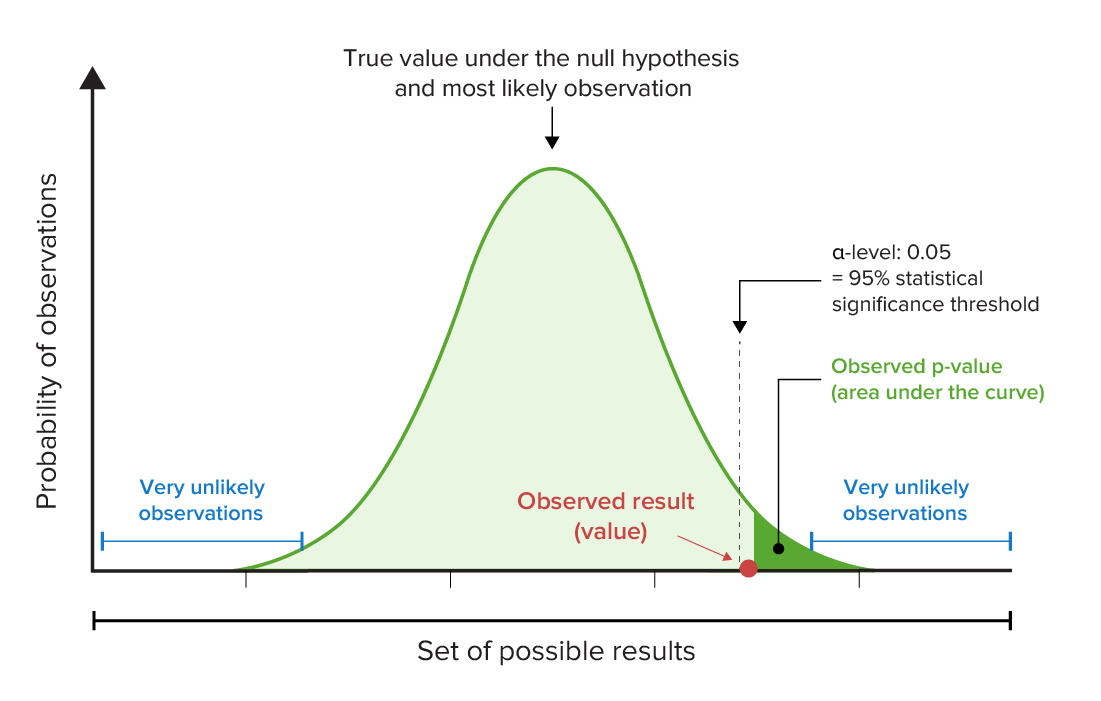
Representação gráfica do p-value e níveis α:
Observe, neste exemplo, que o p-value observado é menor que o nível predeterminado de significância estatística (neste caso, 95%). Isto significa que a hipótese nula deve ser rejeitada porque o resultado observado seria muito improvável se a hipótese nula (de que não existe relação entre as variáveis) fosse verdadeira.
A escolha do teste baseia-se em:
Deve sempre questionar-se a razoabilidade do modelo. Se o modelo está errado, todo o resto também está.
Tenha cuidado com variáveis que não são verdadeiramente independentes.
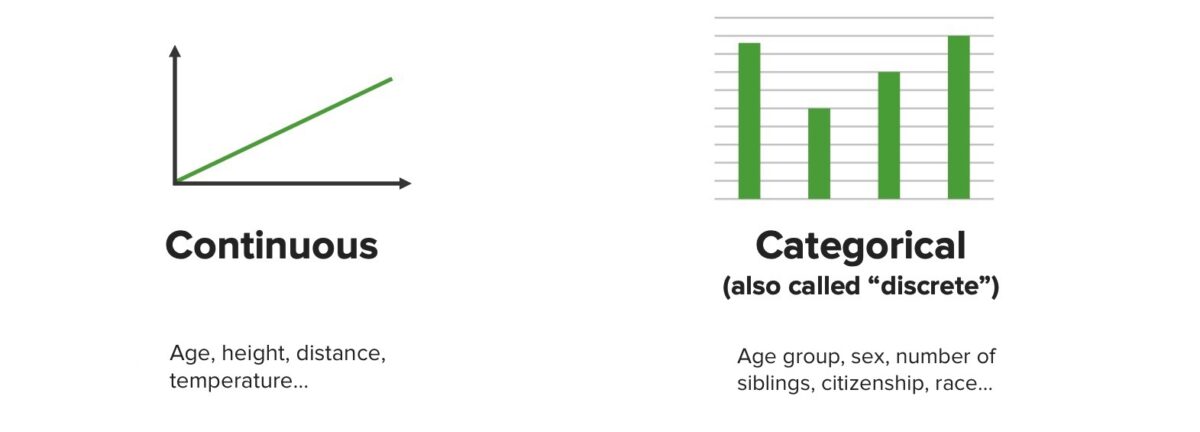
Representações gráficas de dados contínuos e categóricos
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0As 3 categorias principais de testes estatísticos são:
| Nome de teste | O que o teste está a testar | Tipos de variáveis/dados | Exemplo |
|---|---|---|---|
| Testes de regressão | |||
| Regressão linear simples | Como é que uma alteração na variável de previsão/entrada (input) afeta a variável de resultado |
|
Como é que o peso (preditor) afeta a esperança de vida (resultado)? |
| Regressão linear múltipla | Como é que as alterações nas combinações de ≥ 2 variáveis preditoras podem prever alterações no resultado |
|
Como é que o peso e o status socioeconómico (preditores) afetam a esperança de vida (resultado)? |
| Regressão logística | Como é que ≥ 1 variáveis preditoras podem afetar um resultado binário |
|
Qual é o efeito do peso (preditor) na sobrevivência (resultado binário: morto ou vivo)? |
| Testes de comparação | |||
| Teste t (t-test) emparelhado | Compara as médias de 2 grupos da mesma população |
|
Comparar os pesos dos bebés (resultado) antes e depois da alimentação (preditor). |
| Teste t (t-test) independente | Compara as médias de 2 grupos de diferentes populações |
|
Qual é a diferença na altura média (resultado) entre 2 equipas de basquete diferentes (preditor)? |
| Análise de variância (ANOVA) | Compara as médias de > 2 grupos |
|
Qual é a diferença nos níveis de glicose no sangue (resultado) 1, 2 e 3 horas após uma refeição (preditores)? |
| Testes de correlação | |||
| Teste qui-quadrado | Testa a força da associação entre 2 variáveis categóricas com um tamanho de amostra maior |
|
Comparar se a aceitação na faculdade de medicina (variável 1) é mais provável se o candidato nasceu no Reino Unido (variável 2). |
| Teste exato de Fisher | Testa a força da associação entre 2 variáveis categóricas com um tamanho de amostra menor |
|
Igual ao qui-quadrado, mas com tamanhos de amostra menores |
| Teste de r de Pearson | Testa a força da associação entre 2 variáveis contínuas |
|
Comparar como o nível plasmático de HbA 1c (variável 1) se relaciona com os níveis plasmáticos de triglicéridos (variável 2) em pacientes diabéticos. |
Testes de qui-quadrado são usados frequentemente para analisar dados categóricos e determinar se 2 variáveis categóricas estão relacionadas.
Para realizar um teste qui-quadrado são necessárias 2 informações: os graus de liberdade (número de categorias menos 1) e o nível α (que é escolhido pelo investigador e geralmente definido como 0,05). Além disso, os dados devem ser organizados numa tabela.
Exemplo: Se você quisesse ver se os malabaristas eram mais propensos a nascer durante uma determinada estação do ano, os dados poderiam ser registrados na tabela seguinte:
| Categoria (i): estação de nascimento | Frequência observada de malabaristas em cada estação de nascimento |
|---|---|
| Primavera | 66 |
| Verão | 82 |
| Outono | 74 |
| Inverno | 78 |
Para começar, as frequências esperadas para cada célula na tabela acima precisam de ser determinadas usando a equação:
$$ Frequência\ esperada = np_{0i} $$onde n = o tamanho da amostra e p0i é a proporção hipotética em cada categoria i.
No exemplo acima, n = 300 e p0i é ¼, então a frequência esperada em cada célula é 300 * 0,25 = 75 em cada célula.
A estatística de teste é então calculada pela fórmula padrão do qui-quadrado:
$$ \chi ^{2} = \sum _{todas\ as\ células} \frac{(observado-esperado)^{2}}{esperado} $$onde 𝝌2 é a estatística de teste que está a ser calculada. Para cada “célula” ou categoria, a frequência esperada é subtraída da frequência observada; este valor é elevado ao quadrado e depois dividido pela frequência esperada. Depois de este número ser calculado para cada categoria, os números são somados.
Exemplo de cálculo de 𝝌2: Usando o exemplo acima, a frequência esperada em cada célula é 75, então o teste de 𝝌2 pode ser calculada da seguinte forma:
| Categoria (i): estação de nascimento | Frequência observada de malabaristas com cada estação de nascimento | (Observado – esperado) 2 /esperado |
|---|---|---|
| Primavra | 66 | (66 ‒ 75) 2 / 75 = 1,08 |
| Verão | 82 | (82 ‒ 75) 2 / 75 = 0,653 |
| Outono | 74 | (74 ‒ 75) 2 / 75 = 0,013 |
| Inverno | 78 | (78 ‒ 75) 2 / 75 = 0,12 |
𝝌 2 = 1,08 + 0,653 + 0,013 + 0,12 = 1,866
Determinar se a estatística de teste é ou não estatisticamente significativa:
Para determinar se esta estatística de teste é estatisticamente significativa, a tabela de qui-quadrado é usada para obter o número crítico de qui-quadrado.
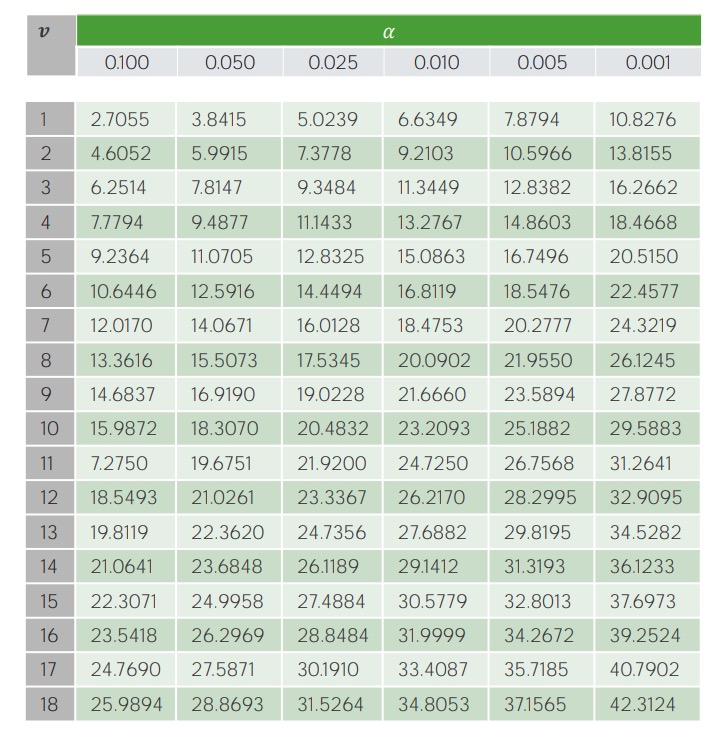
Exemplo da tabela de valores críticos para o teste de 𝝌2:
No eixo y, V representa os graus de liberdade (ou seja, o número de categorias em estudo menos 1); os níveis de significância (níveis α) são mostrados ao longo do eixo x. Os valores críticos correspondentes são encontrados na tabela e comparados com a estatística de teste calculada.
Exemplo de teste 𝝌2: Os malabaristas são mais propensos a nascer numa determinada estação com um nível de significância de 0,05?
| Categoria (i): estação de nascimento | Frequência observada de malabaristas com cada estação de nascimento | (Observado ‒ esperado) 2 /esperado |
|---|---|---|
| Primavera | 66 | (66 ‒ 75) 2 / 75 = 1,08 |
| Verão | 82 | (82 ‒ 75) 2 / 75 = 0,653 |
| Outono | 74 | (74 ‒ 75) 2 / 75 = 0,013 |
| Inverno | 78 | (78 ‒ 75) 2 / 75 = 0,12 |
𝝌2= 1,08 + 0,653 + 0,013 + 0,12 = 1,866
Como 1,866 é < 7,81 (o nosso valor crítico), precisamos de não rejeitar (ou seja, aceitar) a hipótese nula e concluir que a estação de nascimento não está associada ao malabarismo.
Armadilhas comuns:
Semelhante ao 𝝌2, o teste exato de Fisher é um teste estatístico usado para determinar se existem associações não aleatórias entre 2 variáveis categóricas.
Monta-se uma tabela de contingência 2 × 2 assim:
| Y | Z | Total da linha | |
|---|---|---|---|
| W | A | B | A + B |
| X | C | D | C + D |
| Total da coluna | A + C | B + D | A + B + C + D (= n ) |
A estatística do teste, p , é calculada a partir desta tabela usando a seguinte fórmula:
$$ p = \frac{(\frac{a+b}{a})(\frac{c+d}{c})}{(\frac{n}{a+c})} = \frac{(\frac{a+b}{b})(\frac{c+d}{d})}{(\frac{n}{b+d})} = \frac{(a+b)! (c+d)! (a+c)! (b+d)!}{a! b! c! d! n!} $$onde p = p-value; A, B, C e D são números das células numa tabela de contingência básica 2 × 2; e n = total de A + B + C + D.
Antes de ser feito qualquer cálculo, os dados devem ser apresentados num formato gráfico simples (por exemplo, gráfico de barras, gráfico de dispersão, histograma).
Tabelas de contingência:
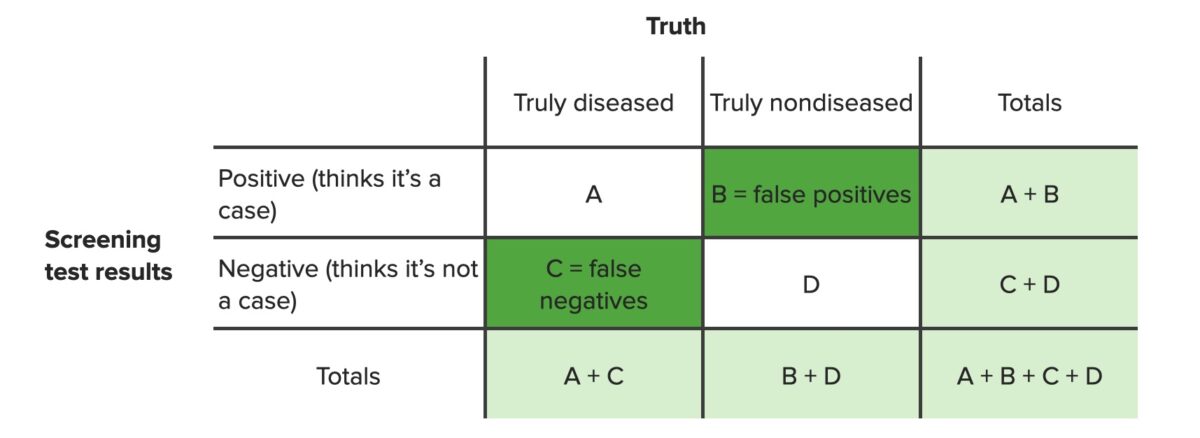
Tabela de contingência identificando falsos positivos (b) e falsos negativos (c)
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0Diagrama de dispersão (scatter diagram):
Gráficos de caixa (box plots):
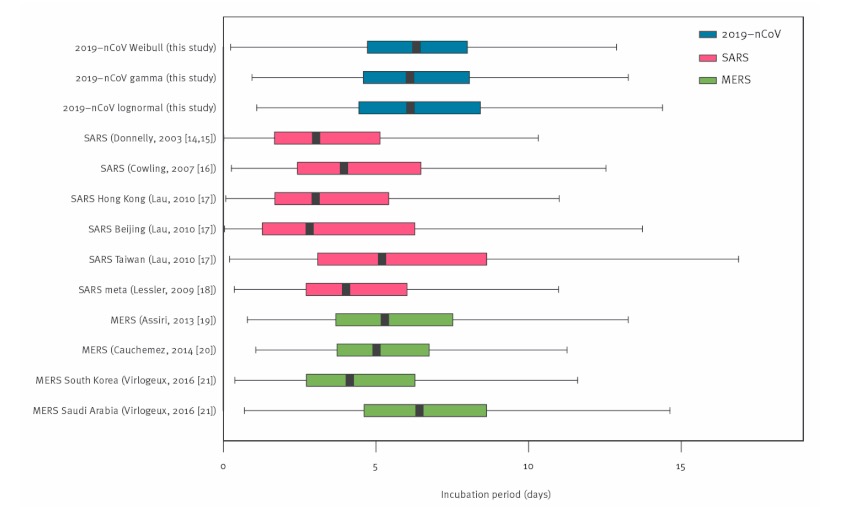
Exemplo de um gráfico de caixa
Imagem: “Box-and-whisker-plots” por Jantien A. Backer, Don Klinkenberg, Jacco Wallinga. Licença: CC BY 4.0Curvas de sobrevivência de Kaplan-Meier
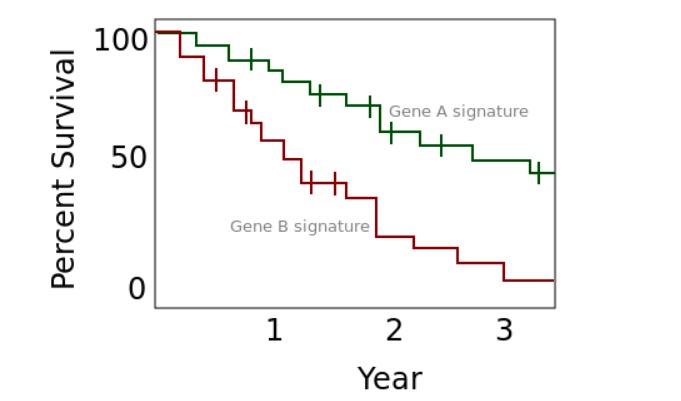
Exemplo de um gráfico de Kaplan-Meier
Imagem: “An example of a Kaplan Meier plot” por Rw251. Licença: CC0 1.0Tabelas (uma tabela de frequência é um exemplo):
Histogramas:
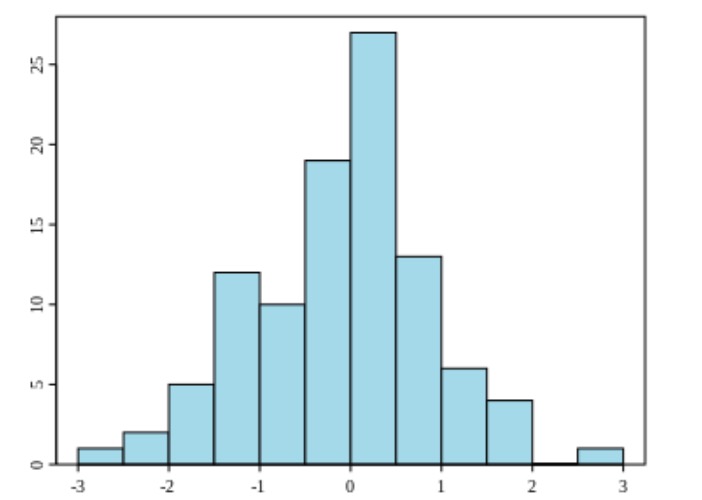
Exemplo de um histograma
Imagem: “Example of a histogram” por Jkv. Licença: Domínio PúblicoGráficos de polígonos de frequência:
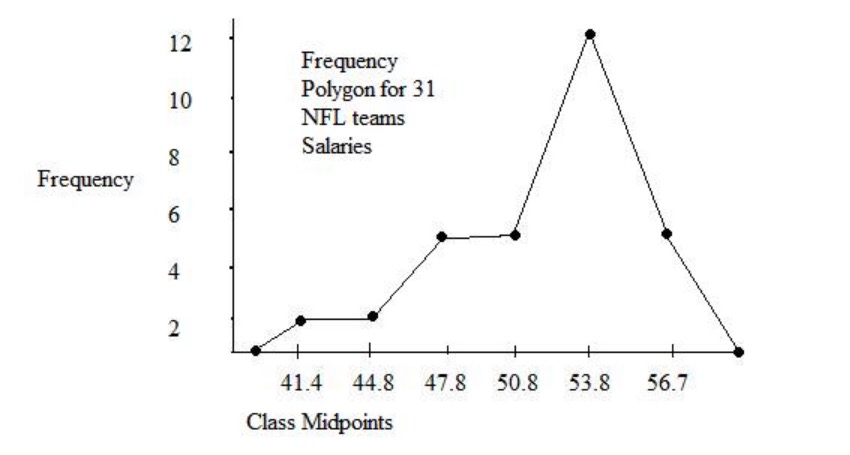
Gráfico de polígonos de frequência para salários de 31 equipes da NFL
Imagem: “Example of a frequency polygon chart” por JLW87. Licença: Public DomainTabelas de frequência, gráficos de barras/histogramas e gráficos circulares são 3 das formas mais comuns de apresentar dados categóricos.
Tabelas de frequência:
| Cor do semáforo | Frequência |
|---|---|
| Vermelho | 65 |
| Amarelo | 5 |
| Verde | 30 |
Gráfico de barras:
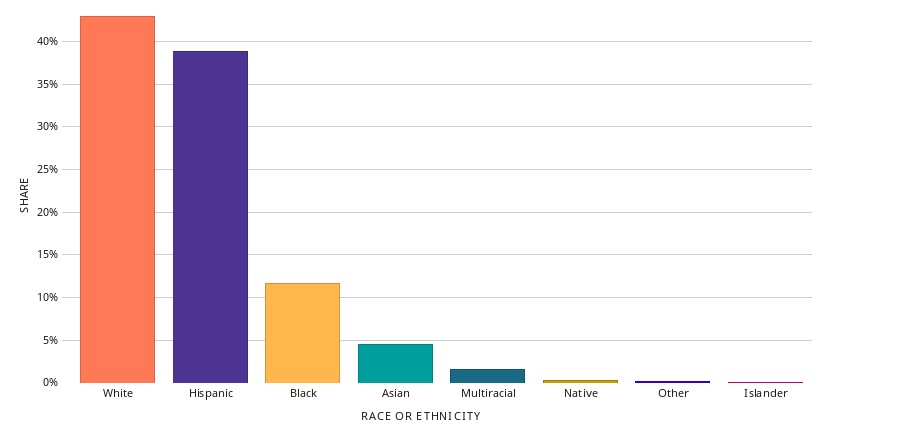
Exemplo de gráfico de barras
Imagem: “Bar Chart of Race & Ethnicity in Texas” por Datawheel. Licença: CC0 1.0Gráfico circular:
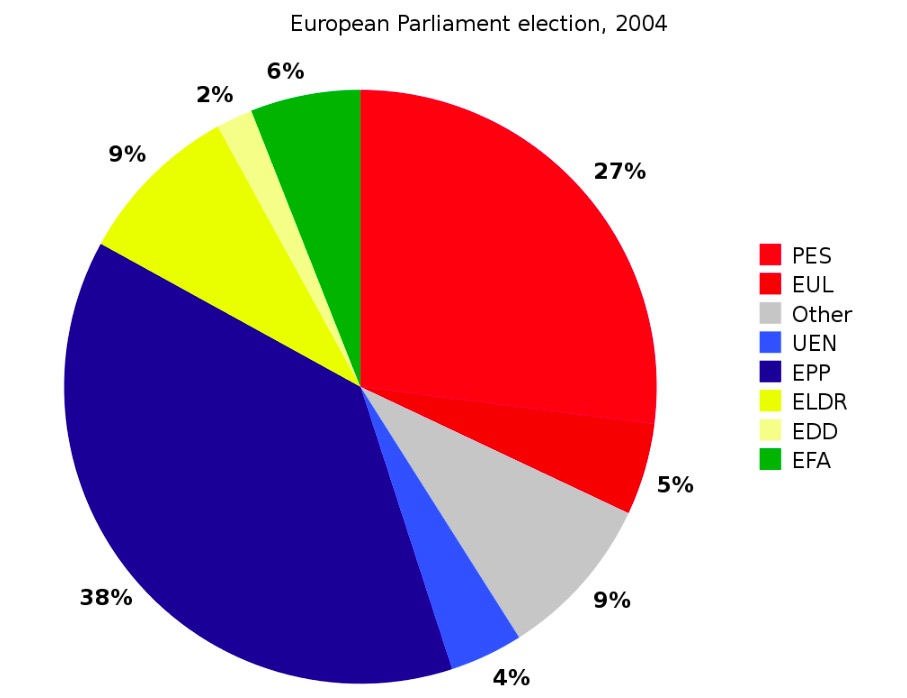
Exemplo de um gráfico circular
Imagem: “A pie chart for the example data” por Liftarn. Licença: Public Domain