Playlist
Show Playlist
Hide Playlist
Introduction to Probability
-
Slides Statistics pt1 Introduction to Probability.pdf
-
Download Lecture Overview
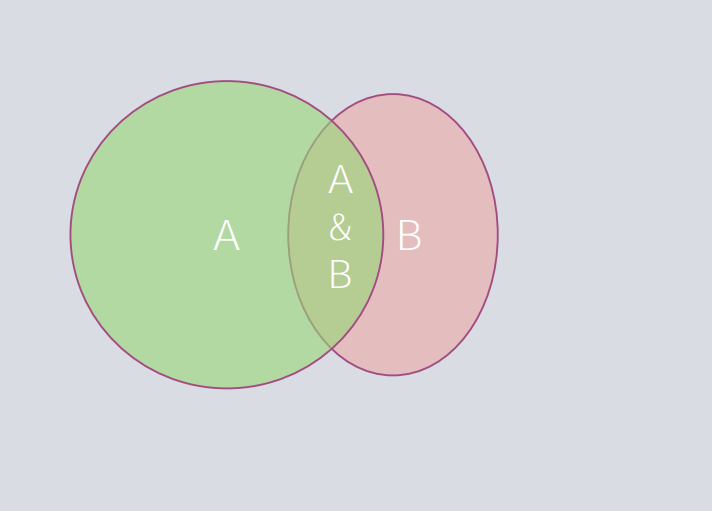
00:01 Welcome back for Lecture 11, where we're going to give an introduction to probability. 00:06 Let's start by looking at random phenomena, and what is going to happen. 00:11 And instead of just giving a formal definition of what are random phenomenon is we're gonna do this by example. 00:18 Let's suppose that we're driving home from work, and you drive through the same intersection every day and you never know whether the lights going to be red, yellow or green when you get there. 00:27 This is an example of a random phenomenon. 00:29 Formally, a random phenomenon is a situation in which the possible outcomes are known but we don't know exactly what's going to happen. 00:38 In each occasion on which we observe a random phenomenon is known as a trial and what occurs during each trial is known as an outcome. 00:48 On the traffic light example we have three possible outcomes, red, yellow or green. 00:53 Red, yellow and green give us an example of what we call a sample space or set of all possible outcomes for a trial. 01:01 For example, if the light is yellow, you might accelerate and go through it and treat it like a green light, or you might hit the brakes treat it more like a red light. 01:12 You may wanna combine the yellow with either the red or the green, a combination of outcomes in this way is known as an event or what we also known as the subset of the sample space. 01:23 We'll denote the sample space by the bold face S for the rest of this lecture. 01:29 Let's look at the law of large numbers and what happened if we do a whole bunch of trials? So the questions is what is the probability that the light is green at this interaction? How can we think about it? Well, the important principle is called the law of large numbers and what it says is that if we repeat a random phenomenon over and over, the percentage of the time or the proportionate of times that the event occurs settles around a particular number. 01:56 And this number that the proportion of times the event occurs settles around is known as the probability of the event. 02:03 We have some conditions that we need for the law of large numbers. 02:07 The first and foremost the most important is that the outcomes have the same probabilities for each trial and that each trial is carried out independently. 02:16 To summarize, the law of large numbers tells us that the number -- as the number of independent trial gets large the long run relative frequency of the repeated events gets closer to a single value that is the probability of the event. 02:30 Lets' look at the law of large numbers versus the often stated law of averages. 02:37 What do people mean when they say law of averages? Well, we hear about it all the time. 02:42 For example, Mike Trout of the LA Angels is batting 325 for this season but hasn't gotten a base hit in 53 consecutive of bats. 02:50 Announcers often say the law of averages say that he's due for a hit. 02:54 Well, they mean the law of large numbers first of all but the law of large number doesn’t say anything about short term behavior. 03:04 It only refers to long run relative frequencies. 03:07 In other words, when they say Mike Trout is due for a hit, no he's not, if we assume the probability of him getting a hit is .325 then over a large number of the bats we would expect him to get a hit 32.5% of the time. 03:21 This doesn’t mean that he's ought to hit this time because he hasn't had one in a while. 03:26 How do we model probability? How do we describe random phenomena? Well, we have several types of probability, sometimes probability comes from a mathematical model and is not necessarily from observation. We call this a theoretical probability. 03:42 Common models are based on games of chance and sometimes people will even assign probabilities to events based on personal feelings. 03:51 For example, you might say if you're taking a particular course, I have a 45% chance of getting an A in this course. 04:00 This is based on a personal feeling and not on observation you haven't taken the course a lot of times to be able to observe some sort of long run behavior. 04:10 These are personal or subjective probabilities because they're not based on observation, they're just based on subjective ideals and personal feelings. 04:19 The message is when you hear a probability stated, you did try to think about what kind of probability it is? When we work with probabilities, we need to sort some things out in order to isolate events and things in that nature. 04:34 It's helpful to make pictures, and the most common types of pictures that we make when we deal with probabilities are known as Venn Diagrams. 04:42 We won't give a formal definition in this lecture but what we will do is point them out each time we use them. 04:48 The first three rules of probability, make a picture, make a picture, make a picture, that sounds familiar. 04:54 You should make a picture for pretty much everything you do in statistics but especially when working with probabilities. But there's more rules of probability. 05:03 In fact there’s five more, and we're gonna through the next five now. 05:06 The first rule is if the probability of an event is 0, the event never occurs. 05:12 If the probability of the event is 1, the event always occurs. 05:16 Formally stated if A is an event and the probability that A occurs which will write, P of A satisfies this in equality, P of A is between 0 and 1. 05:27 The second rule, if a random phenomenon has only one possible outcome it's not very interesting, so we have to distribute the probabilities among the different outcomes a trial might have. 05:40 For example, you're reading a book, and you're on chapter 3 and there's three possible outcomes that are going to happen. 05:47 Outcome A, you reach to the end of the chapter and stop. 05:51 Outcome B, you read a couple more pages and then stops before the end of the chapter, or C you stop reading immediately. 05:59 Something has to happen, so either A, B or C in our example must happen. 06:06 In other words, the probability of something happening is 1. 06:09 What we do is we assign probabilities to individual outcomes in such way that the probability of each outcome, the probabilities of all the outcomes add up to 1. 06:20 In other words, the probability of the entire sample space is 1. 06:24 This is called the probability assignment rule, so formally for a sample space S, P of S is equal to 1. 06:30 We have the compliment rule. Suppose we have an event A that has probability 0.2 of occurring, and then the two possible outcomes are A happens or A doesn't happen. 06:44 The event that A does not happen is known as the compliment of A and we'll note that with A superscript C. 06:50 In this case the sample space is made up of two outcomes, A occurs, A doesn't occur. 06:57 Therefore, the probability that an event does not occur is 1- the probability that the event does occurs, in other words the probability of A compliment is 1- the probability of A and we call this the compliment rule. 07:11 Let's look at a picture of what the compliment rule looks like, here's a Venn diagram and the big box represents the sample space. 07:18 The circle inside the box is A that represents the outcome A, everything else in the box represents A compliment. 07:28 The entire probability in the box is 1, we have the probability of A represented in the circle corresponding to A and then the probability of A compliment represented by everything else. 07:38 The probability of A compliment then is 1- the probability of A. 07:42 Let's look at an example. If the probability that the traffic light is green when you get there is 0.35, what’s the probability that it's not green when we get there? Well, let's let G denote the event that the light is green. 07:55 Then, if we use the compliment rule the probability that the light is not green is the same things as the probability of G compliment which in 1- the probability of G or 1- 0.35 or 0.65. 08:09 In other words, to summarize, the probability that the light is green -- is not green when we get there is 0.65 by the compliment rule. 08:17 Let's look at what happen if we let G be the event that the light is green and Y be the event that the light is yellow. 08:24 What is the probability that the light is either green or yellow? Well, we need to ask ourselves some questions first. 08:32 First, can the light be green and yellow at the same time? Well, no it can't. 08:37 When two events cannot occur at the same time these events are said to be disjoint or mutually exclusive. 08:44 We have an easy rule for finding probabilities for disjoint events, if two events A and B are disjoints then the probability that one or the other occurs written probability write-written P of A cup B which is read probability of A union B or probability of A or B, is equal just simply to the probability of A plus the probability of B. 09:08 Here's a Venn diagram for the probability of disjoint events. 09:13 Again, the big box represent the entire sample space so there’s a probability of 1 corresponding to that whole box. 09:20 The area -- the probability in the circle corresponding to A represents the probability of A. 09:27 The probability in the circle corresponding to B represents the probability of B. 09:32 And note that they don't overlap so the total probability in those two circles is just the probability in a one circle plus the probability in the other circle. 09:42 Let's look at the traffic light example again. 09:46 Suppose the probability that the light is yellow is 0.2. 09:50 What's the probability that the light is either green or yellow? Well, we're gonna use the addition rule for disjoint events. 09:57 Probability of G or Y is equal to the probability of G plus the probability of Y or 0.35 plus 0.32 or 0.55. 10:07 So the probability is either yellow or green with the probability 0.55. 10:13 We can move this rule -- we can generalize it to any number of disjoint events. 10:18 So for example we can use it this to check probability assignments. 10:21 Suppose A, B and C are disjoint events then the probability that the A occurs or B occurs or C occurs is just the probability that A occurs plus the probability that B occurs plus the probability that C occurs. 10:34 What about independent events? We say that two events A and B are independent if the occurrence of A does not have any effect on the probability that B occurs. 10:48 For example if your job requires you to fly from Atlanta to Houston every Monday morning, and the airline's website says that the probability that the flight is on time is 0.85. 10:59 Well, what is the probability that the flight is on time the next two weeks? We're gonna assume that the two flights occur independently. 11:06 What this is question is asking is what is the probability that the flight in on time this week and that it’s on time next week? For independent events, this is an easy question to answer. 11:19 We have a multiplication rule, if two events A and B are independent then probability that both A and B occur which is written P of A cap B or probability of A intersect B is given by P of A intersect B is equal to the probability of A times the probability of B. 11:39 If we let A be the event that this week's flight is on time, and B be the event that next week's flight is on time, then we have that the probability of A is equal to the probability of B is equal to 0.85. 11:52 We assume that A and B are independent, right? That the flights occur independently, so the probability that both flights are on time is P of A and B which is the probability of A times the probability of B or 0.85 times 0.85 or 0.7225. 12:10 In probability there are bunch of things that can go wrong and several pitfalls that we want to avoid. 12:15 We wanna beware of the probabilities that don't add up to 1. 12:19 We don't wanna add probability of events if they're not disjoint and similarly we don't wanna multiply probabilities of events if they're not independent. 12:29 Don't confuse disjoint and independent, they're not the same thing disjoint events cannot be independent by definition because knowing that one occurred tells you that the other one didn't. 12:41 The probability, or one of them occurring tells you that the probability of the other one occurring is zero. 12:48 So disjoint events cannot be independent. 12:50 Don't make the mistake of using the law of large numbers to describe events in the short term. 12:56 Remember the Mike Trout example, where that doesn't mean he's due for a hit. 13:00 And finally, be sure to think about whether or not assuming events are independent is a reasonable thing to do. 13:07 In this section, what we've done is we describe what random phenomenon and probabilities are. 13:14 We looked at some common rules of probability, and we describe some of the issues that can arise when using probabilities, and we also illustrated some of these things in pictures. 13:24 This is the end of Lecture 11, and we’ll see you back her for Lecture 12.
About the Lecture
The lecture Introduction to Probability by David Spade, PhD is from the course Statistics Part 1. It contains the following chapters:
- Introduction to Probability
- Modeling Probability
- The Complement Rule
- Independent Events
- Probability Pitfalls
Included Quiz Questions
What is a property of a random phenomenon?
- In a random phenomenon, the possible outcomes of a trial are known, but it is unknown what will happen on any particular trial.
- In a random phenomenon, it is known what will happen on any given trial.
- In a random phenomenon, the possible outcomes of a trial are unknown.
- In a random phenomenon, the possible outcomes of a trial are known, and it is also known what will happen on each trial.
- In a random phenomenon, it is known what will happen in only one of the many given trials.
What is NOT true about the Law of Large Numbers?
- If an event A has probability 0.9, and it has not occurred in the first 10 trials of a random phenomenon, it is sure to occur on the 11th.
- In order for the Law of Large Numbers to apply, each trial must be carried out independently.
- If we repeat a random phenomenon over and over again, the relative frequency of the occurrence of a particular outcome or event settles around the probability of an event.
- The Law of Large Numbers applies only to long-run relative frequencies.
- The Law of Large Numbers does not apply to short-run relative frequencies.
What is not true about probability?
- If A and B are two events, then P (A) + P (B) must be smaller than 1.
- If the probability of an event is 0, the event never occurs.
- If the probability of an event is 1, the event always occurs.
- If S is the sample space, then P ( S ) = 1.
- If the probability of an event is 0.5, the event sometimes occurs.
Suppose A, B, and C are events such that P (A) = 0. 1, P(B) = 0.2 and P(C) = 0.5. Suppose also that A, B and C are disjoint events. What is the probability that none of them happens?
- The probability that none of these events happens is 0.2.
- The probability that none of these events happens is 0.8.
- The probability that none of these events happens is 0.
- The probability that none of these events happens is 1.
- The probability that none of these events happens is 0.4.
Let A and B be two events. What is NOT something that can be done using the rules of probability?
- If A and B are disjoint events, the probability that both of them will occur can be found by multiplying P(A) and P(B).
- If A and B are independent, the probability that both will occur can be found by multiplying P(A) and P(B).
- If A and B are disjoint events, the probability that one of them will occur can be found by adding P(A) and P(B).
- The P(A) and P(B) must have a value between 0 and 1.
What CANNOT be a probability?
- 8
- 0
- 1
- 0.5
- 0.2
What is the probability that a person would live forever?
- 0
- 1
- 0.5
- 0.2
- 8
What is the probability that a person would NEVER live forever?
- 1
- 0
- 0.5
- 0.2
- 8
What is the probability of getting a 1 when a 6-sided dice is thrown?
- 1/6
- 0
- 2/13
- 1/15
- 2/85
If the probability of event (A) occurring is 0.4, then the probability of event (A) not occurring is what?
- 0.6
- 0.5
- 0.4
- 0.3
- 0.2
Customer reviews
5,0 of 5 stars
| 5 Stars |
|
1 |
| 4 Stars |
|
0 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |
good overview and a clear into to the topic good speaker