Playlist
Show Playlist
Hide Playlist
Brain Stem Components: Midbrain, Pons and Medulla Oblongata
-
Slides 6 BrainStem BrainAndNervousSystem.pdf
-
Reference List Anatomy.pdf
-
Download Lecture Overview
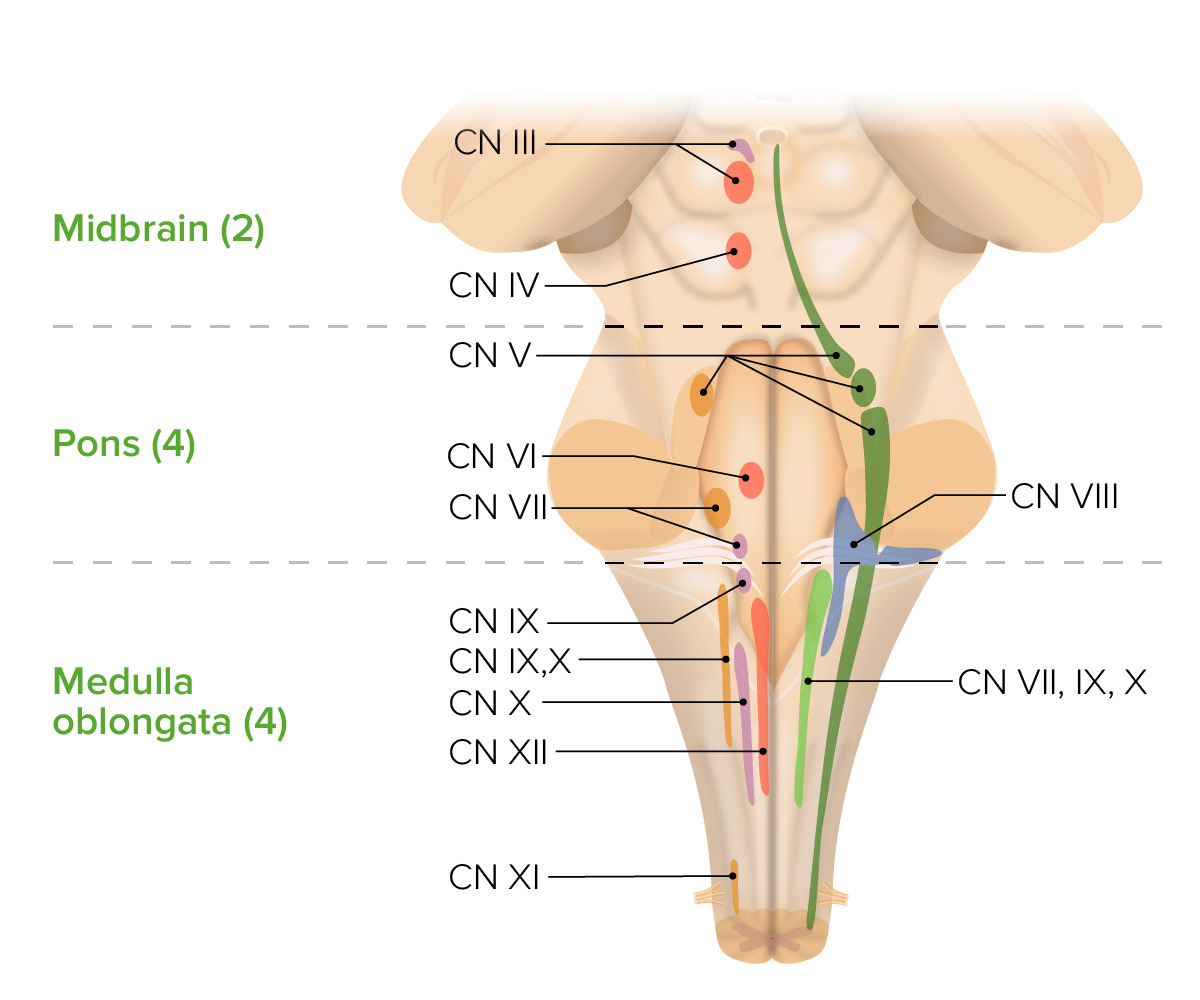
00:00 Welcome to this presentation on the brainstem. The brainstem is made up of three components. 00:07 These three components house very important brain structures such as 10 of the 12 cranial nerve nuclei. 00:14 We’ll find the red nucleus here. We’ll find inferior and superior colliculi and a lot of other importance as we go through this presentation. The first thing that I would like you to realize is what three structures make up the brainstem. On this image, we see the most superior one. That is the midbrain. This area here along in through here. Just below that, we have this expanded area called the pons. Inferior to the pons, you see this shaded area and this is the medulla oblongata. Then it will continue inferiorly as the spinal cord. 00:56 In medical practice, anatomy is seen through imaging studies. Imaging studies of the brain were keenly well-utilized because of their high quality resolution, magnetic resonance imaging. The three structures of the midbrain can clearly be seen in this sagittal MRI section. First, here’s the midbrain right in through here. 01:22 Then this prominent expanded structure is the pons. Then right below that labeled for you is the medulla oblongata. 01:32 Then the spinal cord can be seen extending inferiorly into the vertebral column. Now, I want to guide you through the brainstem origin of cranial nerve nuclei. Ten of the twelve cranial nerve nuclei are housed in the midbrain structures. You can see several of those nuclei in this illustration. Here’s an important concept for you to remember. Here, we’re looking at the origin, the brainstem origin of the cranial nerve nuclei. 02:08 In this illustration, two of the nuclei are housed in the midbrain. Four are housed in the pons area. 02:18 Then four of the cranial nerve nuclei are going to be housed in the medulla oblongata. So it’s two, four, and four. 02:27 Let’s take a look at the two cranial nerve nuclei that are housed in the midbrain. First is the cranial nerve nucleus for cranial nerve III that is shown here in yellow. This gives rise to the oculomotor nerve. 02:49 It’s going to innervate several extraocular eye muscles as well as constrict the pupil. This is an important nucleus for the control of lens accommodation so that we can view objects that are close to us. 03:09 The second and final cranial nerve nucleus that’s found in the midbrain is going to be that associated with the trochlear nerve, so we have cranial nerve IV nucleus. You can see it identified right in through here. 03:24 From this nucleus, the trochlear nerve will leave the posterior aspect of the midbrain. You can see the trochlear nerve right in through here. The trochlear nerve will innervate the superior oblique muscle, one of the extraocular muscles. This now brings us to the level of the pons as we work our way inferiorly. 03:49 Again, remember that the pons has four cranial nerve nuclei. Now, I want you to understand the four nuclei that are located here. The first nucleus to take a look at is actually a paired situation. We’re looking at the trigeminal cranial nerve nuclei. One of them is the motor nucleus of the trigeminal nerve that we see in through here, cranial nerve V motor nucleus. Then over here in blue, we see the sensory nucleus for cranial nerve number V illustrated. The second cranial nerve nucleus that is housed in the pons is going to be that associated with the abducens nerve. This is cranial nerve nucleus number VI right in through here. The next is the cranial nerve VII nucleus. This is the facial nerve nucleus. 04:57 We see it illustrated right in through here. Then the fourth and final cranial nerve nucleus in the pons is going to be that of the vestibulocochlear nerve. Here is the vestibulocochlear nuclear area shown right in through here. Again, these are paired. They’re just visualized on one side to keep this illustration simple and not very confusing for you. So, for the pons, you’re looking at V, VI, VII, and VIII. 05:30 Those cranial nerve nuclei are housed in the pons. Now, this brings us to the medulla oblongata. 05:41 Again, four cranial nerve nuclei are housed here in this brainstem structure. Here you can see some of the cranial nerve nuclei. We’ll take a look at the nuclei that are housed here. First, we have the glossopharyngeal cranial nerve nuclei. This would include the nucleus ambiguus, the inferior salivatory nucleus. 06:06 Then down in through here, we see the solitary nucleus tract. Then the nucleus itself is shown in through here. Now, we’re going to take a look at the vagal nerve nuclei. Some of these nuclei are shared with the glossopharyngeal cranial nerve nuclei. There is a division of labor or division of function. 06:35 So for example, the nucleus ambiguus does communicate. It does send out fibers through the glossopharyngeal nerve. Then the solitary nucleus has a dual function as well with glossopharyngeal and vagus. 06:53 Then we have the cranial nerve X dorsal nucleus being exclusive just to the vagus nerve here. 07:02 Another cranial nerve nucleus that would be more inferior to the illustration that we have here will be the accessory nerve nucleus. This is associated with cranial nerve number XI. Lastly, we have the hypoglossal nerve nucleus that’s labeled here. That would be associated with cranial nerve number XII.
About the Lecture
The lecture Brain Stem Components: Midbrain, Pons and Medulla Oblongata by Craig Canby, PhD is from the course Brain Stem. It contains the following chapters:
- Brain Stem – Components
- Cranial Nerves – Midbrain
- Cranial Nerves – Pons
- Cranial Nerves – Medulla Oblongata
Included Quiz Questions
Which of the following statements about cranial nerve nuclei is most accurate?
- Facial nerve nuclei are found in the pons.
- The olfactory nerve has its nuclei located in the medulla oblongata.
- The vestibulocochlear nerve has its nuclei located in the midbrain.
- The major nuclei of the oculomotor nerve are found in the medulla oblongata.
- The optic nerve originates in the midbrain.
Which of the following muscles is innervated by the trochlear nerve?
- Superior oblique muscle
- Inferior oblique muscle
- Ciliary muscle
- Medial rectus
- Lateral rectus
Customer reviews
3,0 of 5 stars
| 5 Stars |
|
1 |
| 4 Stars |
|
0 |
| 3 Stars |
|
1 |
| 2 Stars |
|
0 |
| 1 Star |
|
1 |
doesnt contain all the information necessary for this topic to be fully understood
good summary and clear presentation with those details are often missed in other review lectures. Good job.
lacklustre explanation and too concise - neuroanatomy is a subject that needs far more explanation even if just a review