Playlist
Show Playlist
Hide Playlist
Renal Tubular Reabsorption and Secretion
-
Slides 05 SecretionPlus UrinarySystem V2.pdf
-
Download Lecture Overview
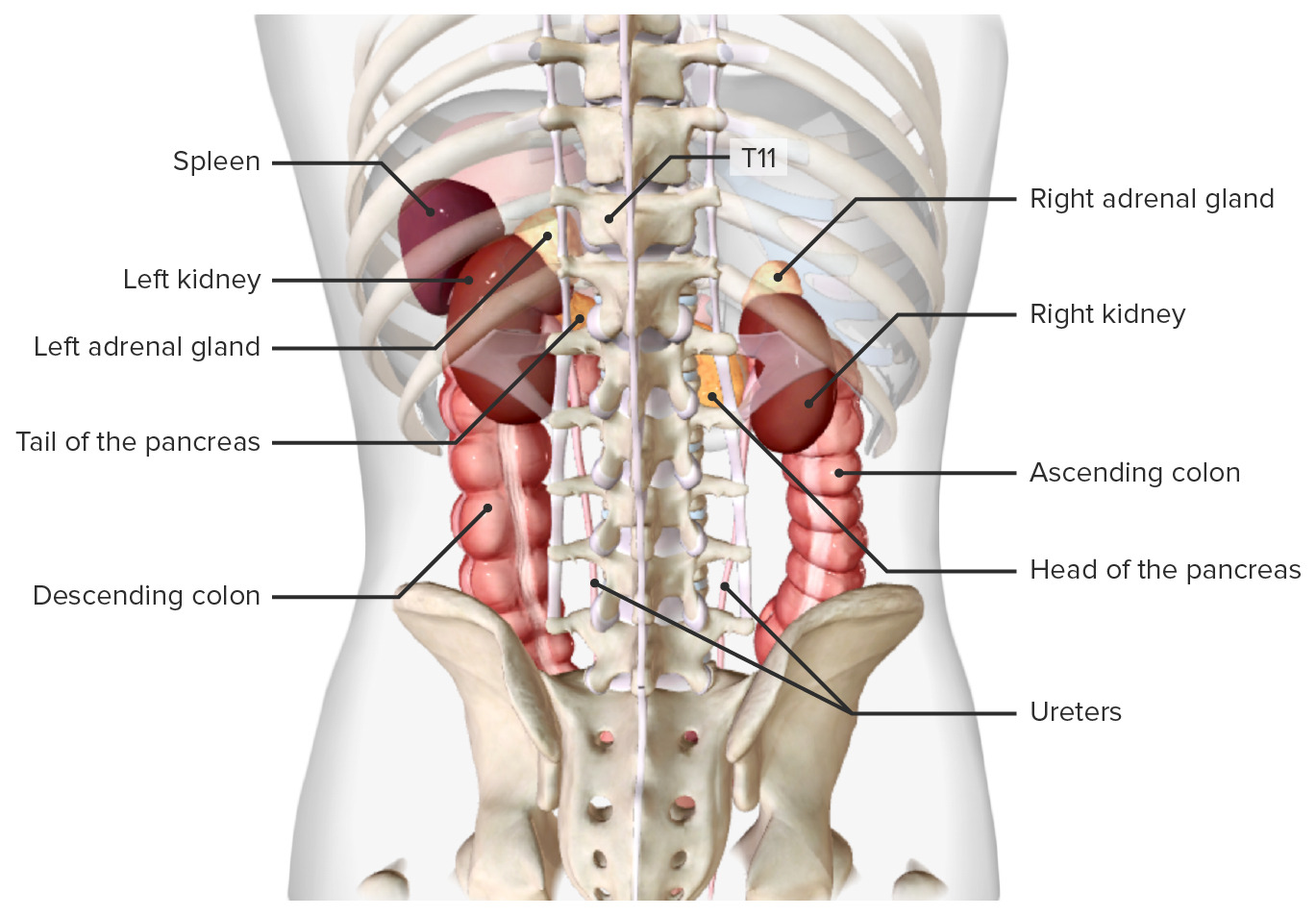
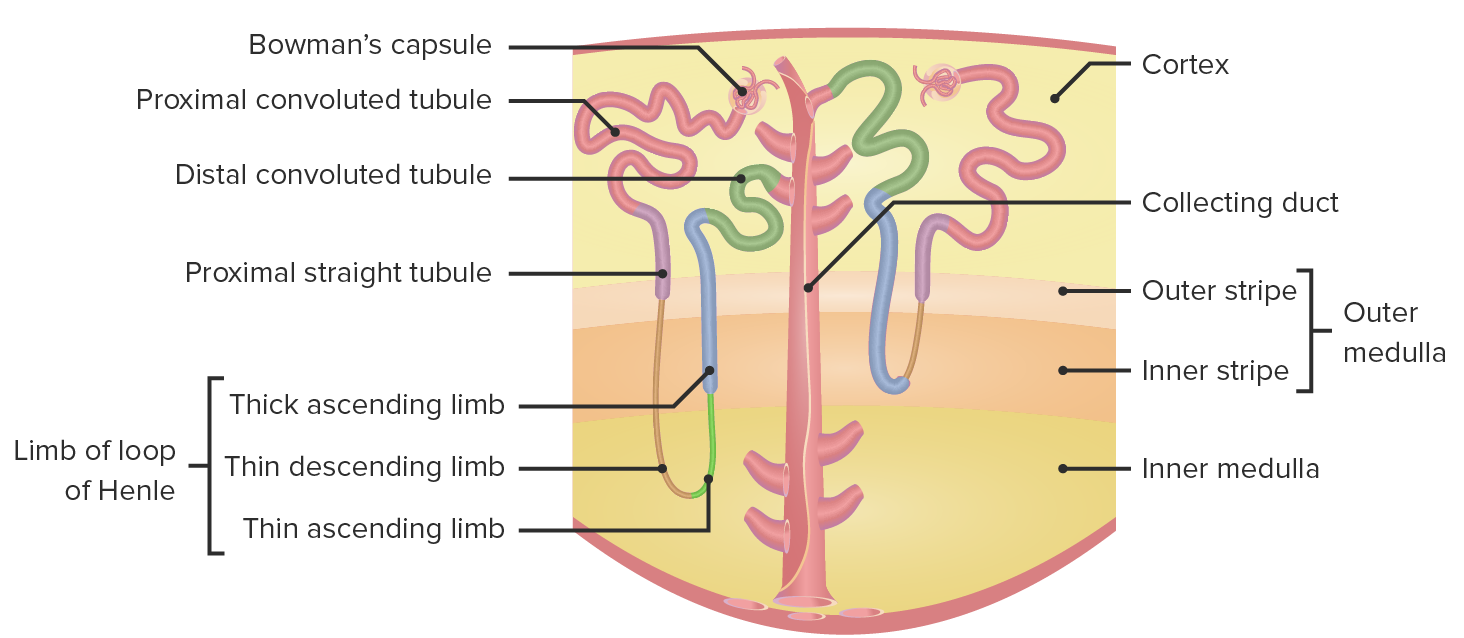
00:00 What you want to start to think about is what areas are involved in the various transport? We talked a lot about the proximal tubule, in fact, the proximal tubule transports somewhere around 120 liters per day of solutes and solvent. 00:19 So it's done a lot of the work. 00:22 But if we break it down on an ion by ion basis, how much movement actually occurs out of the proximal tubule? How much occurs out of the loop of Henle? How much occurs along the thick ascending limb, the distal convoluted tubule and the collecting tubule? So let's take it ion by ion and talk through each of those mechanisms. 00:47 Start with glucose, glucose is primarily absorbed in the proximal, convoluted tubule. In fact, 98 % of all the glucose is reabsorbed by that mechanism. 00:59 The 2 % that's left over is transported out of the proximal straight tubule. So you can see here there's going to be none or very little glucose in the urine. 01:11 And this is based upon that principle that we discussed earlier about a transport maximum. But as long as you have a normal blood glucose level, all of your glucose will be reabsorbed. 01:22 Makes a lot of sense. 01:24 It took a lot to eat that food and get that glucose. 01:27 You might as well keep it in the body and not get rid of it. 01:31 Amino acids and peptides are dealt with in a primarily in a similar manner as glucose, about 99 % of it is reabsorbed in the proximal convoluted tubule and the other 1 % is reabsorbed in the proximal straight. 01:46 That again leaves none to be excreted in a normal, healthy condition. 01:51 Phosphate, another one of our anions to deal with. 01:55 About 80 % of it is reabsorbed in the proximal tubule. 02:00 This is a highly regulated process and that regulation step involves parathyroid hormone. So if you have parathyroid hormone present, you'll block that reabsorption about 10 % of phosphate is reabsorbed in the distal convoluted tubule and then about 10 % is excreted. 02:18 So you notice with this particular anion that you will always lose some phosphate in your urine. 02:28 Urea is an interesting molecule, and about half of it is reabsorbed in the proximal tubule. 02:35 About 30 % of it is reabsorbed in the thick, ascending limb, then about 50 % is reabsorbed in the collecting tubule. 02:45 And I know, I know we have some math wizards out there, 50 plus 50 plus 30. 02:51 That's over 100 %, isn't it? So why do we have over 100 %? We must have it being secreted into the renal tubule somewhere. 02:59 Where does that occur? Where does it occur? Oh, in the loop of Henle; about 50 % occurs in the loop of Henle in terms of secretion. 03:09 So that's how come you can have a greater than 100 % because this is going through the area cycle and allowing for some of that urea to be both reabsorbed and secreted. 03:19 And you end up with still about 40 % in the urine. 03:24 Bicarbonate is one of those really important to anions, we use it for acid base balance, but how we retain this important in that most of it is reabsorbed in the proximal tubule, about 80 %. 03:37 So most all of it is reabsorbed at that point, about 10 % is reabsorbed in the thick ascending limb, about 6 % from the distal convoluted tubule. 03:51 About 4 % occurs in the collecting tubule. 03:55 And that leaves none that is going to be in the urine. 03:59 So even though it occurs in four different spots, the primary portion is in the proximal tubule and then more minor aspects are removed at different other points along the nephron. 04:13 Calcium and magnesium, these two divalent cations are reabsorbed in very similar spots. 04:21 So let's start with calcium. 04:24 About 65 % of it is reabsorbed in the proximal tubule, about 25 % in the thick ascending limb, about 8 % in the distal convoluted tubule. 04:37 And that is highly regulated by parathyroid hormone. 04:40 So if you have parathyroid hormone present, you will reabsorb that calcium. 04:45 If parathyroid hormone is absent, you will have that calcium move past the tubule and end up being secreted. 04:53 About 1 % is reabsorbed in the collecting duct, and that leaves only 1 % in the urine. 05:02 Magnesium is reabsorbed a little bit less, about 15 % of the proximal tubule. But it's real spot of regulation and of reabsorption is in the thick ascending limb. 05:14 And that can be seen here. 05:15 A 70 % is reabsorbed in that account, but that still leaves about 15 % to deal with. 05:22 Where do those occur? 10 % in the distal convoluted tubule. 05:27 And that is primarily regulated by endothelial growth factor. 05:32 And then about 5 % is eliminated in the urine. 05:35 So you see magnesium is lost to a greater degree than calcium. 05:40 Potassium is an important can ion. 05:42 Potassium is a little bit dependent upon how much you intake via diet. So sometimes you will be able to secrete it, sometimes you reabsorb it. So let's go through this complicated process. 05:56 Always you'll have about 80 % reabsorption of potassium in the proximal tubule. 06:02 You'll get a further 10 % in the thick ascending limb. 06:06 So those are constant. 06:07 What does change, though, is how much is secreted in the convoluted tubule and how much is reabsorbed in the collecting duct. 06:15 So let's go through a couple of examples of that. 06:18 If you have a normal diet will be a little bit of secretion, about 10 to 100 % in the convoluted tubing that is primarily controlled by Aldosterone. 06:29 Then you have 5 to 50 % that is reabsorbed in the collecting duct. 06:34 So you notice there's high ranges there. 06:36 Why are those high ranges occur based upon how much dietary potassium you intake? If you don't take in enough potassium or you have a low dietary intake of potassium, you'll want to reabsorb them more. 06:51 And so how do you do this? Well, you reabsorb a bit in the distal convoluted tubule, about 2 % and then about 6 more percent in the collecting tubule. 07:02 So if you take the 80 that is collected through the proximal tubule, the 10 through the thick ascending limb, the two from the distal convoluted tube and the 6 % through the collecting duct, it only leaves you 2 % to excrete. 07:17 That's much different than when you have a normal potassium diet in which as much as 10 to 100 % of the dietary intake could be excreted in the urine sodium. One of our most important diets. 07:31 You always need to think about sodium because where sodium goes, water want to travel along with it. 07:37 So let's go through this important molecule now. 07:40 About 66 % of sodium is reabsorbed in the proximal tubule. 07:45 We learn that that is primarily by a co transport mechanisms with things like glucose and other molecules. 07:53 About 25 % of it is reabsorbed in the thick ascending limb. 07:57 And that is done through these co transporters that involve both chloride and potassium. In the distal convoluted tube, you have another 5 % being reabsorbed and that is done through an exchanger between sodium chloride. 08:12 And finally, about 3 additional percent are reabsorbed in the collecting duct. 08:18 This leads only about 1 % being lost in the urine. 08:22 So sodium is reabsorbed. 08:24 99 % of it in the net from the important regulatory steps involve angiotensin two and angiotensin two. 08:33 It will affect two different regions. 08:36 The proximal tubule and the thick ascending limb. 08:39 Aldosterone affects the distal convoluted tubule regulation. 08:42 And that's that 5 % at that local amp will involve losing more sodium. 08:51 So instead of absorbing more, you'll reabsorb less. 08:54 And AMP is atrial nature peptide. 08:58 So you can say atrial natriuretic peptide and aldosterone work at the same spot and these will be counter regulatory. 09:05 Aldosterone will want to reabsorb and atrial natriuretic peptide will want you to release the sodium. 09:12 The reabsorption of water is one of our most important aspects in the kidney. 09:17 Water regulation involves things like controlling blood volume and controlling body fluid balance. So where does this occur? 66 % is brought off in the proximal, convoluted tubule. 09:28 And if you notice, this matches sodium quite well, then 15 % more is reabsorbed into thin descending limb of the loop of Henle. 09:37 So that yields quite a bit of the reabsorption already occurring. 09:42 Now the last portion is a regulatory step and that is about 18 % of the water is reabsorbed in the collecting to really what are the two regulatory molecules that we need to be involved with here. 09:54 That’s arginine vasopressin, or antidiuretic hormone and that will stimulate this reabsorption of 18 %. 10:02 The counter regulatory hormone in this case is ANP or atrial natriuretic, peptide, and that will reduce the amount of water that is reabsorbed. So 80 H. 10:14 Arginine vasopressin reabsorbed the water. 10:16 ANP allows for more to be released. 10:20 Usually there's only about 1 % of the water in a normal hydrated state that is lost in the urine. 10:28 So 99 % of it is reabsorbed.
About the Lecture
The lecture Renal Tubular Reabsorption and Secretion by Thad Wilson, PhD is from the course Urinary Tract Physiology.
Included Quiz Questions
Where is bicarbonate mainly reabsorbed in the nephron?
- Proximal convoluted tubule
- Thick ascending limb
- Distal convoluted tubule
- Collecting tubule
Where is magnesium mainly reabsorbed in the nephron?
- Thick ascending limb
- Proximal tubule
- Distal convoluted tubule
- Collecting tubule
Where is water mainly reabsorbed in the nephron?
- Proximal convoluted tubule
- Thick ascending limb
- Distal convoluted tubule
- Collecting tubule
Where is phosphate mainly reabsorbed in the nephron?
- Proximal convoluted tubule
- Distal convoluted tubule
- Collecting duct
- Ascending limb of the loop of Henle
- Descending limb of the loop of Henle
Customer reviews
5,0 of 5 stars
| 5 Stars |
|
5 |
| 4 Stars |
|
0 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |