Playlist
Show Playlist
Hide Playlist
Likelihood Ratio – Screening Tests
-
Slides 14 ScreeningTests Epidemiology.pdf
-
Reference List Epidemiology and Biostatistics.pdf
-
Download Lecture Overview
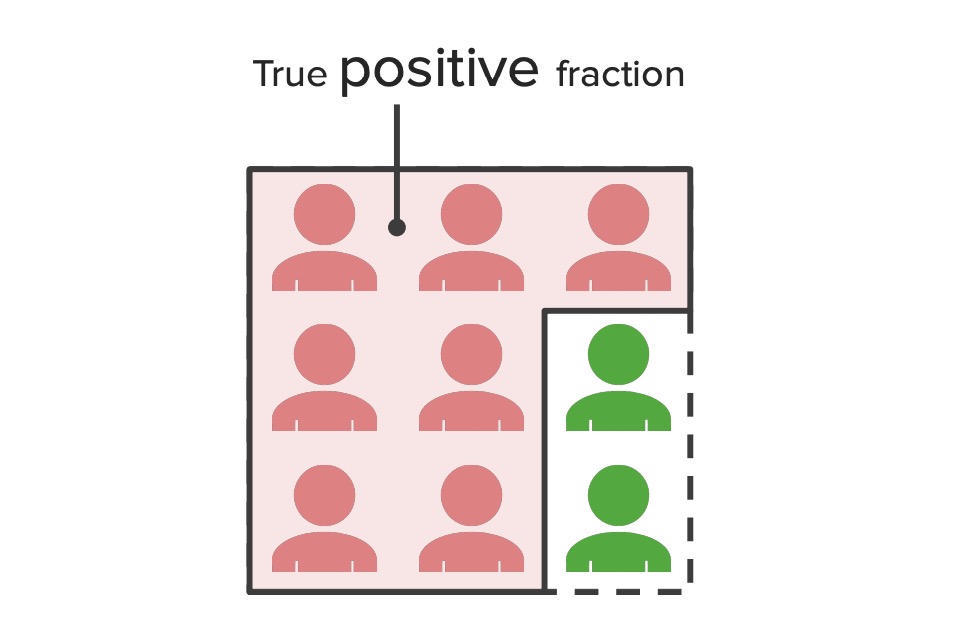
00:01 Keep in mind now that at any given time, everybody has a non zero probability of having a certain disease. Think about the pregnancy example, if you are a heterosexual sexually active women of reproductive age, there is a non zero chance you're probably pregnant. When you take the pregnancy test, we change that probability because the results of the test give us a bit more wisdom about how likely it is that you're probably pregnant or not pregnant. 00:30 In other words we're trying to measure the likelihood that you're pregnant and that brings up a whole new measurement, called the likelihood ratio. The likelihood ratio tells us how much additional information or wisdom a result from a pregnancy test gives us, or screening test gives us relative to not having taken that test, keeping in mind there is always going to be a baseline amount of risk. So a likelihood ratio is a ratio, hence the name, the thing about ratios is they are symmetrical about the number one. If the ratio is one, nothing is going on, if it's more than one, we know that the test result is associated with the presence of a disease. On the other hand, it's less than one, it's associated with the absence of a disease. So again, everything is symmetrical around one, that's what ratios are all about. So a high likelihood ratio or LR+ or positive likelihood ratio, tells us there's a strong suspicion that a positive result from our test means the person has the disease. On the other hand, a low, negative likelihood ratio or LR- tells us we have a strong suspicion that a negative test result means that a person doesn't have a disease, a lot of information there. I've told you about the positive likelihood ratio and the negative likelihood ratio. In reality we tend to only compute the positive likelihood ratio. 01:49 So if you read about likelihood ratios, or LRs, usually the person doing the writing was talking about the positive case, very rarely have I ever seen a negative likelihood ratio used in real life, but I'm going to show you how compute it anyway and we're going to interpret it together. So likelihood ratios tell us how much we should shift our suspicion of a particular test result, or as a result of a test result. We always have some suspicion that an individual has a disease or not, the test result gives us more information that allows us to shift that suspicion one way or the other. So the LR+, the positive likelihood ratio tells us how much to increase our suspicion if they have the disease if the test is positive. 02:34 The LR- or negative likelihood ratio tells us how much to decrease our suspicion if the test is negative. The LR+ is given by the probability of true positives, remember what that means, the people who test positive who actually are positive, divided by the probability of false positives. Remember what that means, false positives are people who test positive, but aren't positive. So in other words the LR+ or positive likelihood ratio is a probability of a positive test result for a person who really has a disease divided by the probability of a positive test result for someone who doesn't really have the disease. It's a lot of words, it's easier if you look up the contingency table and work it out visually, at least I find it that way. Trust me when I say when you mess around with the variables and the arithmetic, the LR+ can be given as a function of sensitivity and specificity, specifically, no pun intended, sensitivity divided by one minus the specificity. Similarly the LR- or the negative likelihood ratio is the probability of false negatives divided by the probability of true negatives. In other words, the probability of a negative test result for a person who really has the disease divided by the probability of a negative test result for someone who doesn't really have the disease. Again I understand if it is confusing, but when we do an example, it'll be clearer. And again, much like the LR+, we can re-express the likelihood ratio as a function of sensitivity and specificity. The LR- is essentially one minus the sensitivity, all divided by the specificity. 04:15 So back to our contingency table, we can use the same table to compute likelihood ratio. 04:22 We have our true positives, our false positives, our false negatives and our true negatives. 04:26 The LR+ given by the probability of true positives divided by false positives. And as I mentioned that can be expressed as a function of sensitivity and specificity. So back to our example of pregnant women. How much more likely is a pregnant woman to test positive than a non-pregnant woman? That is a question of likelihood ratio. Our sensitivity remember, was 0, our specificity was 0, our LR+ is given as a function of sensitivity and specificity and we compute it to be 12.329. Similarly our negative likelihood ratio gives us a number of 0.108. How do we interpret these numbers? It tells us that there is a 12 fold greater likelihood that a woman who tests positive truly is pregnant. So anything over 10 is pretty extreme, some people like to say five is the cutoff, that tells us the test is useful, a positive test result gives me some very useful information that I can use in my clinical practice. Similarly my LR- of 0.1 tells me that a negative test result reduces the odds of being pregnant by 90%. Again we tend not to use the negative likely ratio, usually we're using just the positive one and we tend to call it just the likelihood ratio. 05:46 So let's go over our take home messages. Sensitivity tells us how well a test can detect whether a diseased person truly is diseased. Specificity, similar, but in the reverse, it tells us how well a test can detect whether or not a non-diseased person truly is non-diseased. The positive predictive value tells us how much confidence to put into a test positive result, in other words how precise is the test. And the NPV or negative value tells us the opposite, how much confidence to put into a test negative result. Likelihood ratios tell us how much to shift our suspicion of disease given the test result. So the positive likelihood ratio tells us how much more likely a person with the disease is to have it positive test result, whereas a negative likelihood tells us how much more likely a person without the disease is to have a negative test result.
About the Lecture
The lecture Likelihood Ratio – Screening Tests by Raywat Deonandan, PhD is from the course Screening Tests.
Included Quiz Questions
Which of the following statements is correct regarding the positive likelihood ratio?
- It increases with the increased specificity of the test.
- It is calculated through the equation, LR+ = Specificity/ (1-sensitivity).
- A test with a likelihood ratio close to zero has little practical significance.
- Unlike predictive values, the likelihood ratio is dependent on disease prevalence.
- It is calculated by dividing negative predictive value by positive predictive value.
Which of the following is correct?
- The negative likelihood ratio tells us how much more likely a person without the disease is to have a negative test result, compared to a person with the disease.
- Sensitivity tells us how well a test can detect whether a non-diseased person is truly disease-free.
- Specificity tells us how much confidence to put into a test`s positive result.
- The positive predictive value tells us how much more likely a person with the disease is to have a positive test result, compared to a person without the disease.
- The negative predictive value tells us the probability of a patient actually having the disease when testing positive.
A new rapid strep test has a sensitivity of 90% and specificity of 82%. Which of the following interpretations is correct?
- There is a 5-fold greater likelihood for a patient who tests positive to have streptococcal pharyngitis.
- A negative test result reduces the odds of having streptococcal pharyngitis by 50%.
- This test will identify 87.5% of patients with streptococcal pharyngitis but will miss 12.5% of patients with the disease.
- There is a 5-fold greater likelihood for a patient who tests positive to get streptococcal pharyngitis in the future.
- This test will identify 90% of patients who do not have the disease.
Customer reviews
5,0 of 5 stars
| 5 Stars |
|
5 |
| 4 Stars |
|
0 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |