Playlist
Show Playlist
Hide Playlist
False Positives and False Negatives – Screening Tests
-
Slides 14 ScreeningTests Epidemiology.pdf
-
Reference List Epidemiology and Biostatistics.pdf
-
Download Lecture Overview
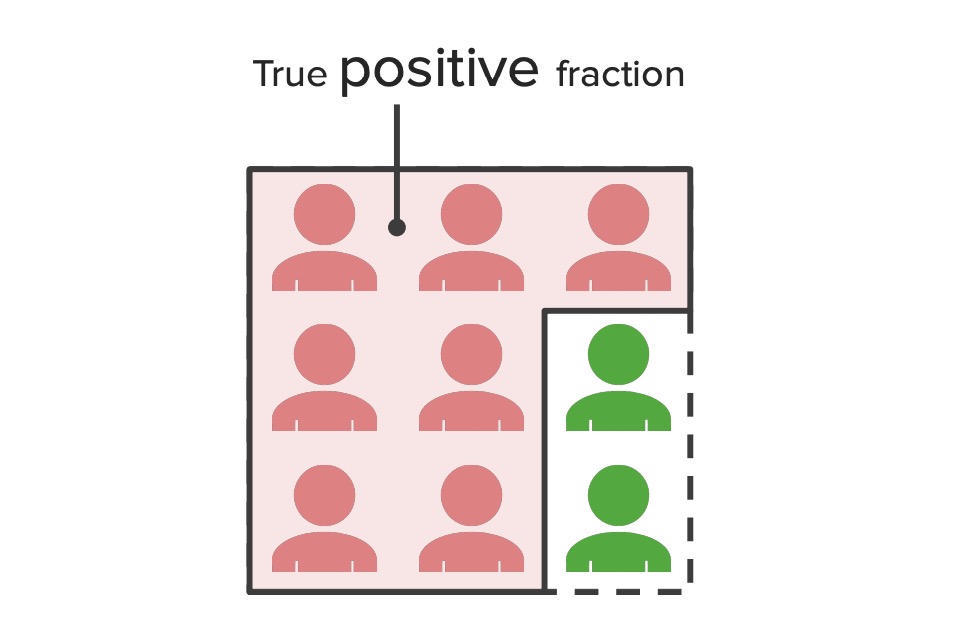
00:00 Now we have to consider this idea of false positives and false negatives. If a test says something as positive and in reality it's a negative, we call that a false positive. 00:12 And if a test says something as negative, but in reality it's a positive, we call that a false negative. It can be confusing, stop to think about that for a second. And false positives and false negatives have certain kinds of burdens in the healthcare system. 00:26 We don't like either one, but some are probably worse than others. Think about this for a second, if you are truly diseased, let's say you have a horrible disease like cancer, but the test finds that you're negative, that's bad, you go about your life not getting the treatment that you need. On the other hand, if you're not truly diseased and the test finds that you are, yes you may worry for a bit, but the follow-up test will confirm that you're truly disease-free. We kind of like the second scenario a bit better in most cases, so we are bit more forgiving towards false positives than false negatives. 01:01 So let's go over the effects of false positives and false negatives. A false positive is a burden on the health care system, because for everyone who is test positive, there's a follow-up, there is a biopsy or an ultrasound or some other kind of expensive deeper investigation, that costs money. Also if you test positive, you're going to be anxious and worry until the confirmation is made that you're actually disease-free. And of course there's the psychological aspects of being told that you are a disease carrier or a diseased individual. On the other hand false negatives, that's pretty serious. That means people are missed being diagnosed when in fact they actually are diseased and they miss perhaps a window for timely early treatment. 01:45 There is also the shock and disbelief when you finally do find out that you are diseased. 01:51 Either one of those are pretty serious considerations and I would argue that's more serious than the negative considerations of false positives. As a result, we like to keep our sensitivity quite high. So which are the false positives in our contingency table? That's going to be B. That's going to be the people who test positive on the screening test, but in reality are negative, in the sense that they're not diseased individuals. Our false negatives are going to those who test negative on the screening test, but in reality are diseased individuals, that's going to be C. So given that we have so many false positives, we need another kind of measurement now, something around precision, i.e. if you test positive on the screening test, what's the likelihood you actually are diseased? We call this the precision rate and there are two kinds of precision rates. There is a positive predictive value and a negative predictive value. So the positive value or PPV or PV+ or precision rate or positive precision rate, there are lots of things to call it, is essentially if a patient tests positive, what's the probability that he or she really has the disease. Similarly, the NPV or negative predictive value or PV-, again, so many different things we can call this, is a probability that if a patient tests negative on the screening test, that he or she really is disease-free. You see the distinction between PPV, NPV and sensitivity, specificity, they're testing subtly different constructs within the context of a screening test. Now my PPV, my positive predictive value is going to be the proportion of everyone who tests positive that are actually diseased. Similarly, the NPV is going be a proportion of anyone who tests negative who are actually disease-free. 03:43 So again back to our contingency table, we always go back here, the PPV can be re-expressed as a function of sensitivity and specificity. If you don't trust me you can do the math yourself, but arithmetically the PPV can be expressed as the product of sensitivity and prevalence, divided by sensitivity times prevalence plus one minus sensitivity times one minus prevalence, that is a lot of words and numbers in there, trust me when I say, that's how the math works out. Similarly the NPV can also be expressed as a function of sensitivity and specificity. 04:16 So if you compute the sensitivity and specificity and you know the prevalence of a disease in your sample, you back compute the PPV, NPV as well or you can do it using first principles from the data on the contingency table. 04:29 So let's summarize what we've learned so far. We've learned the formulas for sensitivity, for specificity, for positive predictive value and for negative predictive value. We've also learned what the prevalence of a disease is on our sample by looking at all the positive test cases, divided by the total sample and we've learned that the PPV and the NPV can also be expressed as functions of sensitivity and specificity. Great, let's work through an example. One of my favorite examples to use when talking about screening tests is a pregnancy test, because it's not an unhappy sort of test to apply. Some people like to use cancer tests; I find that quite depressing, pregnancy is a little more fun. So let's say that 4,810 women take a home pregnancy test, which is essentially a kind of a screening test if you consider pregnancy to be the disease state here, all of them get a follow-up ultrasound scan. Again, in real life they wouldn't, in real life those who test positive for pregnancy would likely go on have an ultrasound, those who test negative likely would not. 05:31 But in this particular study example, everyone goes on to get an ultrasound, so we know what the true state of disease is. In this case disease is not a disease, it's pregnancy. 05:41 So let's look at our data. From our data, 9 women tests positive on a pregnancy test and actually turn out to be pregnant, whereas 1 woman test negative and is actually pregnant. 05:52 351 women on the other hand tests positive on the test and are not pregnant but a whopping 4,449 women tests negative and are indeed not pregnant. Keep in mind this is simulated data, it is not real, it's hypothetical. So I've chosen these numbers to work out a certain way to tell a story, the actual numbers on the back of a pregnant test box may tell a different story. I compute the totals, now let's do our math. So let's ask ourselves, if a woman is actually pregnant, what is the probability that this particular test will also show that she is pregnant, it'll test positive. That's a measurement of, do you know? Sensitivity, that's right. Sensitivity is given by that 9 divided by the total number of people who are actually pregnant. So that's 90%, that's a lot, that's a big number. 06:43 In other words, if a woman is actually pregnant, there is a 90% probability that the screening test will be positive, that's great. Now if a woman is actually not pregnant, but she suspects that she is, so she takes the pregnancy test, what's the probability that the test will show correctly that she is not pregnant, what's that a measurement of? Specificity. 07:05 Alright let's compute our specificity, that's going to be given by 4,449 divided by everyone who truly is not pregnant, that gives us 0, in other words, 92,7% of women, there is a probability that if she isn't actually pregnant the test will show that she isn't pregnant. 07:27 Right. Now if a woman tests positive on a pregnancy test, what is the probability that she is actually pregnant? Do you see the nuanced difference between this question and the first one? We're asking it differently now, if you test positive on the test, what's the probability that she actually is pregnant. So imagine a woman has tested positive on this test, maybe she's excited, maybe she is not excited, depending upon her lifestyle choices and she's going to now follow up with her ultrasound technician to see if in fact she is truly pregnant. This is a measurement of PPV, positive predictive value. We computer our numbers and we get 2,5%, in other words, if a woman screens positive for pregnancy, there is actually only a 2,5% probability that she actually is pregnant. Remember, this is made up numbers, this is not the way the actual pregnancy test would probably play out. And if a woman is tested negative on a pregnancy test, what's the probability that she really is not pregnant? What's this? Negative predictive value, obviously. So I plug in my numbers into my formula and I get 99,9%. So if a woman screens negative, there is a 99,9% chance she's actually not pregnant. 08:40 Now think about this if it wasn't pregnancy, let's say we're talking about something a bit more dire, like cancer or something equally as frightening, we would want our NPV to be as high as possible. We want to be almost 100%, so that if you test negative, you can be pretty certain that you haven't got the disease, we don't want you walking away from the clinic or wherever you got the test thinking you're disease-free when you're not. So a high NPV is fantastic, it tells me this is probably a very good test.
About the Lecture
The lecture False Positives and False Negatives – Screening Tests by Raywat Deonandan, PhD is from the course Screening Tests.
Included Quiz Questions
You estimate that the patient in your office has a one in four chance of having a serious disease. You order a diagnostic test with a sensitivity of 95% and specificity of 90%. The result comes back positive. Based on all the information available, what is the chance of the patient to really have the disease?
- 76%
- 80%
- 91%
- 95%
- 90%
You order a diagnostic test with a sensitivity of 95% and specificity of 90% for a particular disease. What is the probability that the test will come back negative in a patient who does NOT have the disease?
- 90%
- 5%
- 12%
- 20%
- 0%
A screening test is developed for disease X. What do we call the probability that the test will correctly identify someone who truly does not have disease X?
- Specificity
- Sensitivity
- Prevalence
- Positive predictive value
- Negative predictive value
A new diagnostic test is tested on 100 known cases of a disease, and on 200 controls known to be free of this disease. Ninety of the cases yield positive tests, as do 30 of the controls. How many false positives and false negatives did this diagnostic test yield, respectively?
- 30, 10
- 90, 170
- 10, 30
- 170, 90
- 100, 200
Customer reviews
4,0 of 5 stars
| 5 Stars |
|
0 |
| 4 Stars |
|
1 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |
The lecturer is great! My concepts seem to be a lot clearer. However, the answers to the quiz questions need to be displayed somewhere, as i found them quite tough.